Dos pruebas de hipótesis sobre la geografía de las patentes en México

 

Two hypothesis tests for the geography

of patents in Mexico

 

Carlos Javier Vilalta-y Perdomo

Humberto Banda-Ortiz*

 

Abstract

 

In this paper we describe the technological innovation geographical patterns and processes in Mexico. We present the detection and measurement of a spatial concentration pattern of patent applications in Mexico together with a moderate process of spatial spreading, the rejection of the hypothesis of a patenting activity with a physical distance dependent diffusion and the presence of spatial heterogeneity in the sample, as well as their statistical implications.

 

Keywords:  patents, spatial diffusion, spatial autocorrelation, technological development.

 

Resumen

 

En el presente artículo se describen los patrones y procesos geográficos que sigue la innovación tecnológica en México. El estudio ofrece como hallazgos la detección y medición de un patrón de concentración espacial de solicitudes de patentes en México simultáneamente con un proceso moderado de desconcentración espacial, el rechazo de la hipótesis de una difusión dependiente de la distancia física de la actividad patentiva, y la presencia de heterogeneidad espacial en la muestra junto con las implicaciones estadísticas resultantes.

 

Palabras clave: patentes, difusión espacial, autocorrelación espacial, desarrollo tecnológico.

 

 

* Instituto Tecnológico de Estudios Superiores de Monterrey (itesm), Campus Santa Fe. Correos-e: carlos.vilalta@cide.edu, humberto.banda@itesm.mx.

 

 

Introducción

 

En el ambiente empresarial y en el desarrollo económico regional la innovación y las patentes son el resultado de procesos que combinan elementos de la cultura organizacional, la investigación, la transferencia de tecnología y la especialización. Desde la perspectiva global y de política pública, es clara la importancia que tiene el desarrollo tecnológico a través del establecimiento de sistemas nacionales de innovación y el impulso a la economía del conocimiento (Morales y Vilalta, 2007). Estos sistemas de innovación buscan articular a los agentes económicos para la generación, utilización y difusión de las innovaciones con el objetivo de lograr una ventaja competitiva. De manera típica, las innovaciones se convierten en patentes y son éstas la unidad básica de medición de la innovación tecnológica en el mundo (Morales y Vilalta, 2007).

Al igual que las patentes aumentan en el mundo, la investigación sobre las mismas también se ha incrementado. Son y han sido muchos los investigadores dentro de las ciencias sociales y administrativas que tratan de resolver preguntas generales o muy particulares. Sin embargo, geográficamente hablando, ni la teoría clásica sobre la difusión y adopción de las innovaciones establecida por Everett Rogers (1962), ni los enfoques de la macroeconomía sobre los paradigmas tecnológico-económicos y sus procesos de hegemonización (Mandel, 1986; Schumpeter, 1939), ni los importantes estudios sobre el valor relativo o determinante del impacto tecnológico en el medio social (Elster, 1990) consideran el análisis de la circulación y adopción de las innovaciones y/o patentes.

En este sentido, el objetivo de este estudio es conocer la geografía de las patentes en México, particularmente en dos aspectos típicos del análisis espacial: los niveles y patrones de concentración, así como los procesos de difusión. Para este efecto, lógicamente realizamos dos pruebas estadísticas de hipótesis, construyendo sobre teorías generales geográficas y que son la primera ley de la geografía de Tobler (1970) y la teoría de la difusión contagiosa (Hagerstrand, 1953), respectivamente.

Además de esta introducción, el artículo se divide en cuatro partes. La primera contiene un resumen de las diferentes teorías relevantes acerca del desarrollo de las innovaciones tecnológicas desde el punto de vista económico y geográfico. La segunda parte presenta las hipótesis, los datos y la metodología estadística que sigue el estudio. En la tercera parte se muestran y explican los resultados de los análisis estadísticos. En la cuarta y última parte se discuten los resultados y se definen las conclusiones del estudio.

 

1. Estudios previos: la innovación industrial y sus formas geográficas

 

Este apartado contiene una síntesis de los estudios más relevantes sobre las teorías del desarrollo de las innovaciones industriales, donde nos centramos en los aspectos geográficos del fenómeno, en especial en su concentración y difusión espaciales.

Cabe iniciar explicando una diferencia importante entre los conceptos de invención e innovación. Para Joseph Schumpeter (1939) y otros teóricos de la economía, innovaciones e invenciones son cosas particularmente diferentes. Quizá Horst Siebert (1969) da la mejor definición cuando explica de manera precisa que una innovación es la transformación de un proceso potencial en un proceso real, mientras que una invención es la introducción de un nuevo proceso de producción en un conjunto de procesos potenciales. En este sentido y desde el punto de vista geográfico, existen numerosos trabajos que abordan sistemáticamente el estudio de las innovaciones y de las invenciones. Con base en la definición anterior y revisando estos estudios, podemos hacer una distinción y clasificación de investigaciones que siguen 1) un enfoque interdisciplinario geografía-economía o 2) un enfoque puramente geográfico.

Dentro del enfoque geográfico-económico hay estudios que se pueden considerar clásicos, por su relevancia y edad, que han probado empíricamente la relación entre innovación industrial y el desarrollo económico de las regiones. Esta relación se ha explicado desde varias perspectivas teóricas, que ordenadas cronológicamente son las siguientes: la teoría clásica de la localización (Weber, 1929), la teoría del crecimiento de polos (Perroux, 1950) y los modelos de desequilibrio entre regiones (Myrdal, 1957).

Empezando con la teoría clásica de la localización, Alfred Weber (1929) encontró una concentración geográfica de la innovación y del desarrollo y la explicó con base en las variaciones geográficas, ambientales y, particularmente, en los costos de transporte. A partir de lo anterior desarrolló una serie de modelos que explican las posibles combinaciones de factores regionales y locales que influyen en los procesos de toma de decisiones de localización de diferentes industrias. Para este autor, la lógica de localización industrial se basa en la consecución del costo mínimo de producción para alcanzar una eficiencia técnica en el uso de factores productivos. Las críticas a esta teoría se centran en una abstracción inflexible de sus enunciados y en la incapacidad para explicar de manera exhaustiva la localización espacial contemporánea que se caracteriza por la flexibilidad y la globalización.

Por otro lado, la teoría del crecimiento de polos (Perroux, 1950) se enfoca en explicar cómo suceden las inversiones en industrias con un gran impulso (polos de crecimiento), ubicadas en lugares estratégicamente convenientes, y cómo estas inversiones provocan el crecimiento de otras industrias, así como de otras regiones económicas, que no necesariamente son contiguas geográficamente. A partir de esto, Perroux (1950) habla de centros de desarrollo y del incremento en el ingreso de las regiones donde se hallan dichas industrias de punta. Esta perspectiva ha tenido un gran efecto en la elaboración de políticas industriales, como es el caso de México.[1] Esta teoría también predice que el crecimiento no se da de manera uniforme, sino que se concentra precisamente en ciertos polos de desarrollo e industrias impulsoras, con lo cual explica la necesidad de impulsar el liderazgo de algunas empresas y/o industrias en el proceso de desarrollo económico. Este liderazgo se basa en su dimensión, su valor agregado o en la naturaleza estratégica de su actividad industrial.

Finalmente, los modelos de desequilibrio de Myrdal (1957) indican un énfasis en el carácter multidisciplinar del análisis del desarrollo económico regional. Desde este enfoque, se fundamenta la importancia de los aspectos políticos, institucionales y sociológicos que impulsan el proceso de avance económico de una sociedad, generando y facilitando un proceso de causación circular. De manera muy simplificada, el principio de causación circular de Myrdal (1957) explica que en los países económicamente desarrollados el ingreso y la tasa de ahorro son mayores frente a los países subdesarrollados, lo que a su vez genera (circularmente) más tasas de reinversión de capital y mayores tasas de crecimiento, lo que al final provoca una mejor distribución del ingreso.

Como se mencionó, en la literatura científica también están presentes un grupo de estudios que analizan desde un punto de vista estrictamente geográfico los procesos de innovación industrial y sus productos resultantes: las patentes. Estos estudios se enfocan en explicar cómo dichos procesos están sujetos a una dimensión espacial o a reglas geográficas. Dos de estas reglas geográficas son la concentración espacial y la difusión espacial contagiosa. Estas reglas geográficas son evidentes y teóricamente importantes, por lo que vemos que se desarrollan con cierta fuerza estudios urbanos y regionales basados en teorías definidas como de tiempo-espacio (Urry, 1996), y que tienen una preferencia metodológica por la modelación estadística (Vilalta, 2003a). Estos modelos estadísticos enfatizan los aspectos de localización e interacción entre los individuos y las organizaciones en lugares diferentes (Anselin, 1998). Al respecto, Vilalta (2003a) explica que la difusión espacial se refiere a la propagación de ideas o comportamientos de un lugar a otro; naturalmente esta propagación también puede incluir objetos. La difusión espacial ya se ha analizado empíricamente desde hace tiempo (Cliff y Ord, 1981) y se observan cuatro formas elementales: contagio, expansión, relocalización y difusión jerárquica (Hornsby, 2003). La difusión contagiosa sucede cuando la propagación se hace de manera directa y con el contacto entre individuos (por ejemplo, enfermedades virales), lo que hace que este tipo de difusión requiera una proximidad física. La difusión por expansión sucede cuando la propagación de la idea, comportamiento u objeto empieza en un lugar de origen y se difunde a nuevos lugares pero siguiendo su uso o aplicación en su lugar de origen (por ejemplo, invenciones). En cambio, la difusión por relocalización sucede cuando la propagación en cuestión también se esparce desde una fuente a nuevos lugares, pero ahora dejando el lugar de origen de manera temporal o definitiva (como en el caso de los emigrantes). Por último, la difusión jerárquica sucede cuando la propagación va de lugares más grandes a lugares más pequeños, por ejemplo de ciudades grandes a pequeñas o de áreas urbanas a rurales (similar a las invenciones).

En relación con esto, Torstern Hägerstrand (1953, 1966) encontró que la difusión de innovaciones tecnológicas tiende a ser del tipo contagioso. Es decir, la difusión de una innovación es producto de un efecto espacial que está sujeto a una función de contigüidad o proximidad física. Este hallazgo conlleva una noción teórica importante y es que la difusión de las innovaciones implica una dependencia espacial, la cual se ha definido –y sucede estadísticamente– cuando “el valor de la variable dependiente en una unidad espacial es parcialmente función del valor de la misma variable en unidades vecinas” (Flint et al., 2000: 4). Esto se conoce en el análisis estadístico como autocorrelación espacial.

Desde esta perspectiva y observando la presencia de patrones geográficos de concentración de los fenómenos naturales y sociales, Waldo Tobler (1970) definió la primera ley de la geografía que estipula, básicamente, que las cosas cercanas son más similares entre ellas que las que están alejadas; o lo que sucede en un lugar no es independiente de lo que sucede en otros lugares, especialmente los más cercanos (Vilalta, 2003a).

Llevando a nuestro objeto de estudio –las patentes– estas reglas geográficas de difusión espacial, en conjunción con la primera ley de la geografía, implican dos cosas: que la innovación tecnológica se difunde 1) de manera contagiosa –en función de la distancia– y 2) que se halla concentrada en ciertos lugares y de ahí se difunde. Ya Michael Storper (1997) mencionó que mundialmente la producción de conocimiento está muy concentrada espacialmente.

En cuanto a esto, nótese aquí la diferencia crucial que hay entre un proceso de desconcentración espacial y un proceso de difusión espacial contagiosa. El primero puede suceder sin el segundo, pero no a la inversa. Es decir, un fenómeno o proceso de desconcentración espacial de alguna variable social, por ejemplo, de la actividad inventiva, implica una nivelación o disminución de las diferencias regionales, pero no necesariamente implica un proceso de contagio entre las regiones.[2] Hipotéticamente, una región puede ponerse al nivel de otras regiones innovadoras sin que hubiera un efecto o relación entre ambas. En cambio, es importante notar que la difusión contagiosa sí requiere simultáneamente la existencia de una relación espacial-temporal entre las regiones y una nivelación o desconcentración espacial del fenómeno.

Como mencionamos, si bien este enfoque e ideas están sustentadas en evidencia empírica y tienen una secuenciación lógica, es interesante notar que no sobran los estudios empíricos y estadísticos espaciales sobre la difusión de la innovación per se; esto es, análisis sobre cómo y a qué velocidad se difunde tal actividad innovadora. En estos estudios, el indicador más utilizado para medir dicha actividad son las patentes y se concentran en la experiencia de los Estados Unidos. Estos estudios evidencian una concentración espacial de las patentes y de sus inventores, las cuales se deben principalmente a una concentración espacial de la producción industrial, pero en un proceso de difusión. Históricamente se ha encontrado para este país una propagación de esta actividad innovadora entre regiones.

En Latinoamérica se han realizado algunos estudios académicos que tratan el tema de la innovación industrial y las patentes. Hay un grupo de estudios reducido, pero de alta calidad, que se ha abocado a analizar, por ejemplo, los avances en la capacidad innovadora empresarial en Colombia, aun en ambientes de crisis económicas, restricciones crediticias y disminuciones en la inversión en investigación y desarrollo (Malaver y Vargas, 2004). Asimismo, existen discusiones teóricas importantes y acertadas sobre la relación necesaria entre la actitud empresarial para innovar, la integración de redes de conocimiento y el uso racional de los recursos (Caravaca et al., 2005; Méndez, 2002).

Nuestra revisión de la literatura académica en México encuentra un incipiente interés en el tema de la innovación científica al tratar diversos temas paralelos al nuestro y, también, la síntesis de discusiones sobre los sistemas regionales de innovación y sus indicadores (Morales y Vilalta, 2007) y sobre si es global o local la innovación (Rózga, 2003). En sus publicaciones, Enrique Düsell et al. (1997) plantean la arquitectura conceptual de los sistemas regionales de innovación y concluyen que debido a que la coordinación económica entre los países está aumentando, las relaciones entre las empresas en sus respectivos clusters industriales se van regionalizando de manera progresiva.[3]

Otro estudio interesante es el de Arellano et al. (2004), donde encontramos cómo se plantean los aspectos epistemológicos de la globalización de ciertas actividades tecnológicas, como serían los polímeros y los alimentos transgénicos. El estudio de López (2003) también es relevante en la región porque expone claramente el comportamiento de los empresarios –sinaloenses– en la adopción de innovaciones y la dificultad que enfrentan en cuanto a la carencia de políticas gubernamentales, de capital y el efecto adverso de la falta de competencia comercial.

En las ciencias administrativas también existen algunos estudios que, precisamente desde una perspectiva empresarial, caracterizan y miden la trayectoria de la tecnología, la producción y el mercado. En estos estudios las variables de tipo tecnológico utilizadas son las patentes, y entre las no tecnológicas, están el tipo y el volumen de sus productos, la participación de mercado, la penetración de la marca (Arjona, 1995) y la madurez del sector económico en el que se compite por medio de innovaciones (Torres y Jasso, 2003).

Con base en las ideas previas, a continuación describimos la metodología, la cual se divide entre las diferentes hipótesis que se derivan de los estudios revisados, los datos y las técnicas estadísticas que sirven de sustento para estos efectos.

 

2. Metodología: hipótesis, datos y técnicas estadísticas

 

En este estudio probamos estadísticamente las siguientes dos hipótesis de tipo geográfico para el caso de México.

 

1) La innovación tecnológica, medida por las solicitudes de patentes, tiene un patrón espacialmente concentrado.

2) La innovación tecnológica, medida por las solicitudes de patentes, se halla en un proceso de desconcentración dependiente de la distancia.

 

Evidentemente la hipótesis 2 requiere probarse en dos pasos: primero realizar la detección de un proceso de desconcentración y, segundo, que es dependiente de la proximidad geográfica. Las técnicas utilizadas para realizar las pruebas de hipótesis son: 1) el coeficiente de autocorrelación espacial I de Morán (1950) y 2) un análisis de regresión ordinario de mínimos cuadrados (ols). En detalle, el procedimiento en relación con cada hipótesis se indica en el cuadro 1.

 

Cuadro 1

Técnicas para las pruebas de hipótesis

 

Fuente: Elaboración propia.

 

En relación con la hipótesis 2, recuérdese que puede haber un proceso de desconcentración espacial sin una difusión contagiosa y viceversa. Es decir, el fenómeno o proceso de desconcentración espacial no necesariamente implica una relación espacial-temporal entre áreas geográficas.

 

Cuadro 2

Variables utilizadas en el análisis estadístico

 

Para probar estas hipótesis geográficas, operamos los conceptos discutidos previamente en las variables y mediciones indicadas en el cuadro 2. Para el cómputo de los coeficientes de autocorrelación espacial, nos interesó utilizar los datos con que contamos para los tres años estudiados: 2000-2002. En cambio, para el análisis de regresión, la vd es el cambio en el número total de solicitudes de patentes. La medición utilizada para probar la hipótesis de la desconcentración dependiente de la distancia es la sumatoria de la vd en los estados vecinos de cada entidad federativa o estado del país (N = 32). La información sobre patentes proviene de las bases de datos del Instituto Nacional de Estadística, Geografía e Informática (inegi), disponibles en la Internet.

En cuanto a las técnicas estadísticas utilizadas, el coeficiente I de Morán (1950) es la técnica más frecuentemente utilizada en el análisis espacial inferencial.[4] Esta técnica toma la siguiente forma matemática:

 

 

Donde:

·       n es el número de elementos (estados) en la matriz de distancia-vecinos,

·       W_ij es la matriz de vecinos que define si un estado i y j son vecinos o no (el denominador da el número total de vecinos,

·       x es la variable en cuestión, en este caso patentes por estado de residencia del inventor.

 

Para el cálculo del coeficiente I de Morán, en esta investigación se definió a los estados vecinos de dos maneras diferentes: vecinos de primer orden y vecinos de primer orden ajustados. En el primer caso, la matriz de vecinos considera estrictamente como tales a aquellas unidades geográficas contiguas. En el segundo caso, el procedimiento sigue dos pasos: primero la matriz incluye como vecinas a aquellas unidades que son contiguas y posteriormente calcula el promedio de distancias (centroide a centroide) que hay en el conjunto de unidades geográficas, e incluye como vecinas a aquellas unidades que están igual o por debajo de ese promedio. La razón de realizar este ajuste es que el criterio estricto de contigüidad no considera otra dimensión espacial fundamental: la cercanía física. En México, dos unidades geográficas como serían las entidades federativas, pueden estar muy cercanas físicamente pero no ser contiguas (Vilalta, 2003b).

En cuanto al análisis de regresión, se utilizó la técnica de mínimos cuadrados utilizada ampliamente en la literatura especializada por lo que no se considera necesario hacer una explicación mayor al respecto en este inciso. Sin embargo, sí cabe comentar que se utilizaron dos modelos en ecuaciones diferentes, que se diseñaron, y los coeficientes calculados de la siguiente manera:

 

·       Modelo 1 (M1): incluye al Distrito Federal (N = 32)

·       Modelo 2 (M2): excluye al Distrito Federal (n = 31)

 

La ecuación de regresión lineal simple para ambos modelos es:

 

(y_t - y_t-1 ) = β₀ + Wβ₁ y_t-1 + ε_t

 

·       Donde:

       y_t = solicitudes de patentes en 2002

       y_t-1 = solicitudes de patentes en 2000

       β₀ = constante

       Wβ₁= Lag espacial-temporal sobre la vd

       ε_t = error aleatorio

 

La razón de incluir o excluir al Distrito Federal como unidad en el análisis se debe a nuestro deseo de conocer detalladamente el impacto de este estado en la capacidad de los modelos para predecir cambios en el ámbito nacional. Como veremos más adelante, este estado posee alrededor de 40% de las solicitudes de patentes, por lo que su presencia o ausencia en el modelo representa un efecto significativo en los coeficientes, tal y como se demostrará más adelante. Además de lo anterior, se agregan las implicaciones estadísticas de contar con una observación influyente u outlier. Sin embargo, estamos conscientes de que en el análisis espacial no podemos prescindir de unidades geográficas ya que representan áreas con grupos de población reales (Vilalta, 2003b).[5]

 

3. Resultados

 

Esta parte de resultados se divide en dos incisos: estadística descriptiva y estadística espacial e inferencial. Estos resultados se analizan en la parte sobre discusión y conclusiones.

 

3.1. Estadística descriptiva

 

Se puede ver que hay una fuerte concentración de solicitudes de patentes en el Distrito Federal y el Estado de México, representando ambas entidades alrededor de 50% de la capacidad inventiva del país (cuadro 3), y les siguen los estados de Jalisco y Nuevo León. Hay entidades que no producen o solicitan ninguna patente o bien que no rebasan las dos solicitudes, como son los casos de Baja California Sur, Campeche, Chiapas, Tlaxcala y Zacatecas. Cabe mencionar que el número absoluto de patentes aumentó en el periodo estudiado así como la desviación estándar; significando esto último, un mayor alejamiento o diferenciación entre los estados.

 

Cuadro 3

Número de solicitudes de patentes por estado de residencia del inventor

Fuente: Cálculos propios con datos del inegi.

 

Los mapas que presentamos a continuación muestran la productividad en patentes de cada estado medida en desviaciones estándar; es decir, en términos de dispersión y relativos frente a las otras entidades.

 

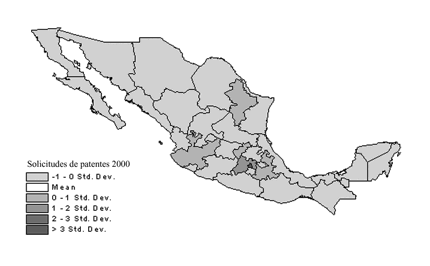
Mapa i

Solicitudes de patentes en 2000

(en desviaciones estándar)

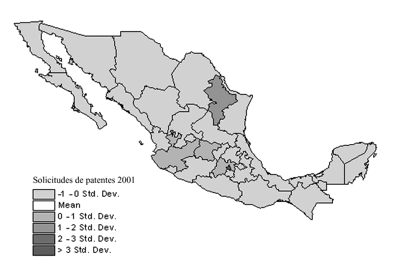
Mapa ii

Solicitudes de patentes en 2001

(en desviaciones estándar)

Mapa iii

Solicitudes de patentes en 2002

(en desviaciones estándar)

 

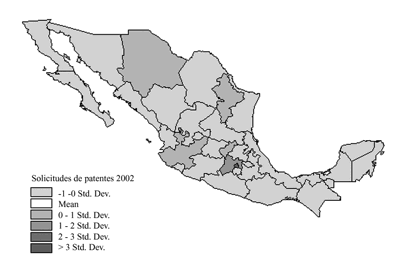
De la observación de estos mapas se desprende fácilmente la preeminencia constante sobre el promedio nacional de entidades como el Distrito Federal, Estado de México, Jalisco, Nuevo León, y ocasionalmente Puebla, Guanajuato, Querétaro y Chihuahua, precisamente los estados más industrializados y urbanizados. La virtud de utilizar en los mapas la desviación estándar es que también permite observar con claridad la poca diferencia u heterogeneidad que hay entre el resto de los estados poco productivos en patentes; es decir, la mayor parte de éstos no difiere mayormente del promedio nacional.

 

3.2. Estadística espacial e inferencial

 

En cuanto a la prueba de la hipótesis 1 que predice una concentración espacial de las solicitudes de patentes, los resultados nos sugieren la aceptación de tal hipótesis (cuadro 4). Es decir, efectivamente la actividad en patentes se halla espacialmente concentrada en todos los años analizados.

 

Cuadro 4

Resultados del análisis de autocorrelación espacial*

* Variable dependiente: número total de solicitudes de patentes por estado de residencia del inventor y el cambio. Elaborado con los datos del cuadro 1.

^** La significancia estadística es una prueba Z de dos colas sobre una distribución teóricamente normal.

 

En relación con la prueba de la hipótesis 2, en su primer paso, se encuentra bajo la definición de vecinos de primer orden ajustado, un proceso de desconcentración espacial a través del tiempo. Esto lo sugiere el decrecimiento progresivo en la magnitud de los coeficientes entre 2000 y 2002. Aunque cabe decir que el cambio (D) en el número de solicitudes de patentes en el periodo no se halla espacialmente concentrado (p = 0.180). Es decir, el cambio en el número de solicitudes de patentes en los estados mexicanos fue independiente o no estuvo relacionado con los cambios en sus estados próximos y bajo ninguna definición utilizada de vecindad geográfica.

Prosiguiendo con la prueba de la hipótesis 2, a continuación mostramos los resultados del modelo de regresión para la prueba de la desconcentración dependiente de la distancia en sus dos formulaciones diferentes: La primera incluye al Distrito Federal y la segunda lo excluye.

 

Cuadro 5

Resultados de la regresión ols sobre M1 incluyendo al

Distrito Federal*,**

 

 

En cuanto al primer modelo (M1) que busca la prueba de la hipótesis sobre el proceso de una desconcentración dependiente de la distancia, podemos observar que no se acepta la hipótesis respectiva de un efecto lag espacial-temporal (p = .493). Esta variable lag espacial-temporal intenta demostrar, sin lograrlo, el efecto de la actividad de patentes de los estados vecinos en cada entidad en el año 2000 hacia el cambio entre 2000 y 2002.

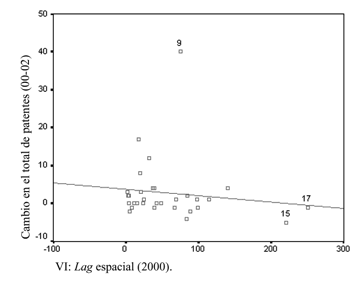
Es importante explicar que M1 considera dentro de la muestra al Distrito Federal y utiliza los datos de solicitudes de patentes en porcentajes por estado y sin normalizar. Cabe señalar esto porque en la gráfica i mostramos el diagrama de dispersión de los estados mexicanos en cuanto a las dos variables utilizadas en este modelo, y lo que observamos son varias entidades que se alejan sobre el eje “x”, como son el Estado de México (15) y Morelos (17), y sobre el eje “y” el Distrito Federal (9). Este último contribuye a aumentar el lag espacial-temporal a favor de sus vecinos Estado de México y Morelos.

 

Gráfica i

Diagrama de dispersión de las solicitudes de patentes (2002) y su lag espacial (2000)

 

Estadísticamente hablando, lo importante de distinguir este fenómeno de outliers entre los estados es que los coeficientes de la línea de regresión obtenida a través del método de mínimos cuadrados pueden ser imprecisos. La presencia de una observación, en este caso un estado, afectando el cómputo de los coeficientes se ve en la gráfica ii, donde se observa al Distrito Federal alejado del resto de los estados y mostrando un comportamiento no normal de los residuales; un prerrequisito del análisis de regresión. También muestra que la ecuación resultante de este modelo no predice correctamente el comportamiento de la vd para tal entidad federativa.

 

Gráfica ii

Histograma de los residuales de M1*

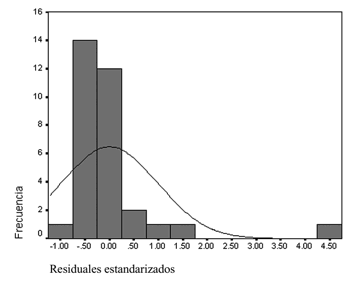
*M1 incluye al Distrito Federal.

 

La gráfica iii es similar a la i pero se distingue en que representa residuales y valores predichos estandarizados de M1. Igualmente muestra los residuales correspondientes al Distrito Federal (marcado como el estado 9 y alejado sobre el eje “x”) y los estados de México y Morelos (15 y 17, respectivamente, y alejados sobre el eje “y”). Los residuales son estimaciones de error o distancias en el ajuste de los datos a la línea de regresión entre dos valores: los observados y los predichos de la vd modelada. También representan una forma de estimar la variación no explicada por el modelo elegido.

 

Gráfica iii

Diagrama de dispersión de los residuales de M1*

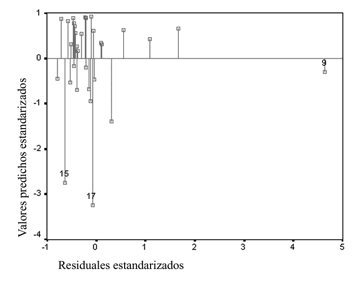
* Incluye al Distrito Federal.

 

Los resultados de M2 se muestran en el cuadro 6. Recordemos que M2 excluye al Distrito Federal en el cómputo de los coeficientes para observar el efecto de su ausencia en la ecuación. Aquí podemos ver que la capacidad predictiva de M2 es considerablemente mayor a la de M1 (R² = .105); aunque en términos generales es baja y queda mucha variación sin explicar, como es natural.[6] La exclusión del Distrito Federal mejora la capacidad predictiva del modelo para el resto de los estados.

 

Cuadro 6

Resultados de la regresión ols sobre M2 excluyendo al Distrito Federal*,**

 

 

Lo más importante en relación con la hipótesis 2 es que es probable la existencia de un efecto espacial-temporal (p = .076). La magnitud del efecto es muy bajo (b = -0.023), pero su signo negativo es revelador puesto que sugiere una contracción o concentración espacial de la actividad de patentes, en oposición a una difusión contagiosa entre los estados del país, pero sólo cuando no se considera la influencia del Distrito Federal en el resto de los estados. Igual que en el caso de M1, M2 presenta dos outliers que nuevamente resultan ser los estados de México y Morelos (gráficas iv y v).

 

Gráfica iv

Histograma de los residuales de M2*

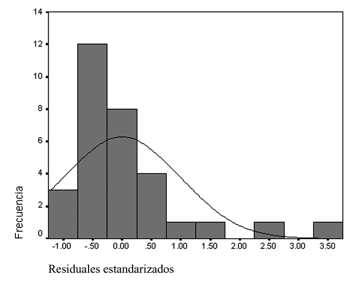
*M2 excluye al Distrito Federal.

 

Gráfica v

Diagrama de dispersión de los residuales de M2*

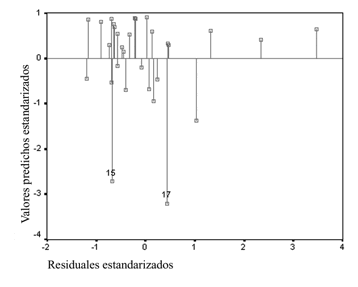
*M2 excluye al Distrito Federal.

 

4. Discusión y conclusiones

 

El análisis realizado en este trabajo nos muestra un patrón espacial de concentración de la actividad de patentes en México; es decir, que las solicitudes de patentes por estado de residencia del inventor se concentran en ciertos estados y grupos de estados en la República Mexicana: Distrito Federal, Estado de México, Jalisco y Nuevo León, los cuales tienen alrededor de 70% de las solicitudes todos los años.

Junto con un patrón espacial de concentración se detectó un proceso de desconcentración espacial o nivelación entre las regiones del país entre 2000 y 2002. Progresiva y moderadamente, la concentración de la actividad de patentes en el país fue disminuyendo. Los incrementos en la proporción nacional de solicitudes de patentes en los estados de Nuevo León y Chihuahua, y los descensos en los estados de México, Puebla y Querétaro explican esta nivelación geográfica nacional.

En cuanto a nuestra hipótesis de una desconcentración espacial dependiente de la distancia, obtuvimos resultados diferentes según el modelo que utilizáramos. El M1, que incluye al Distrito Federal en el análisis de regresión, no ofrece evidencia de algún efecto espacial-temporal, por lo que con base en tal modelo, se procede a rechazar la hipótesis de una desconcentración espacial de la actividad de patentes dependiente de la distancia.

El M2, que excluye al Distrito Federal en el análisis de regresión, ofrece información que incluso no esperábamos encontrar: un proceso de contracción espacial dependiente de la distancia. Es decir, la exclusión del Distrito Federal y su preeminencia en la actividad de patentes evidencia un proceso de divergencia o disparidad regional en tal actividad, explicada por el alejamiento de los estados más productivos en solicitudes de patentes, que son el Estado de México, Jalisco y Nuevo León, de las demás entidades del país.

En términos de teoría económica regional, esto es indicio probable de que el país se sigue polarizando entre estados ricos y pobres, y hace referencia a la idea de los clubes regionales de convergencia económica mencionados en estudios regionales de México (Vilalta, 2003b).[7] En este caso, la divergencia económica regional se refleja en aquellos estados o grupos de estados que implementan nuevas tecnologías por medio de la solicitud de patentes, y aquéllos que se van quedando atrás y aislados de tales desarrollos.

Lo anterior también nos lleva a una conclusión metodológica importante, y es que este fenómeno puede poseer un patrón de heterogeneidad espacial (he) en nuestro objeto de estudio. La he se define por un cambio en las relaciones de las variables de una región o lugar a otro (Lesage, 1998). Es decir, estamos capturando procesos regionales desiguales al interior de un país, lo cual es procedente y no debe sorprender dentro del análisis geográfico (Vilalta, 2003a). Sin embargo la he implica, en términos estadísticos, pendientes de líneas de regresión diferentes para cada región –en este caso grupos de estados mexicanos–, versus cuando utilizamos toda la base de datos del país (Vilalta, 2006). Esto lo vimos al momento de comparar M1 y M2, los cuales se distinguen por la inclusión o exclusión del Distrito Federal en cada modelo. En el primer caso no era detectable un efecto espacial-temporal entre los estados, mientras que en el segundo sí lo era. Cabe mencionar que el efecto estadístico de contar con heterogeneidad espacial en un análisis de regresión es que los coeficientes serán inestables (Vilalta 2006; Anselin, 1998).

En síntesis, nuestra contribución fundamental es detectar y medir una desconcentración espacial demostrativa de un proceso de nivelación geográfico moderado en la actividad de patentes. Además, encontramos que este proceso es independiente de la distancia y que sucede a través del plano nacional, en estados no vecinos y, en relación con Myrdal (1957), con una capacidad endógena para producir o solicitar tales patentes, y que son estados con altos niveles de ingreso e industrialización comparativamente en el país.

Quedan por realizar más pruebas de hipótesis. Se requieren series de tiempo mayores, incorporar otros tipos de técnicas estadísticas espaciales como los coeficientes de autocorrelación locales (Vilalta, 2007), utilizar diferentes niveles de unidades muestrales –por ejemplo ciudades–, analizar los efectos de la he en el fenómeno de la geografía de las patentes y llevar a cabo estudios comparativos con otros países latinoamericanos.

 

Bibliografía

 

Aguilar, Ismael (1993), Descentralización industrial y desarrollo regional en México: una evaluación del programa de parques y ciudades industriales, 1970-1986, El Colegio de México, México.

 

Anselin, Luc (1998), Spatial econometrics: Methods and models, Kluwer Academic Publisher, Dordrecht.

 

Arellano, Antonio, Claudia Ortega y Rubén Martínez (2004), “¿Es global o local la investigación?: la proliferación situada de polímeros, transgénicos y colectivos”, Convergencia: Revista de Ciencias Sociales, 11(35), Universidad Autónoma del Estado de México, Toluca, México, pp. 133-169.

 

Arjona, Luis (1995), “La tecnología en la teoría del comercio: la perspectiva evolutiva”, El Trimestre Económico, 12(284), Fondo de Cultura Económica, México, pp. 435-465.

 

Caravaca, Inmaculada, Gema González y Rocío Silva (2005), “Innovación, redes, recursos patrimoniales y desarrollo territorial”, Revista eure, Pontificia Universidad Católica de Chile, Santiago de Chile, 31(94), pp. 5-24.

 

Cliff, Andrew y Keith Ord (1981), Spatial Processes: Models and Applications, Pion Limited, Londres, Inglaterra.

 

Elster, Jon (1990) El cambio tecnológico. Investigaciones sobre la racionalidad y la transformación social, Gedisa, Barcelona, España.

 

Düssel, Enrique, Clemente Durán y Michael Piore (1997), Pensar globalmente y actuar regionalmente. Hacia un nuevo paradigma industrial para el siglo xxi, Universidad Nacional Autónoma de México-Jus, México.

 

Flint, Colin, Mark Harrower y Robert Edsall (2000), “But How Does Place Matter? Using Bayesian Networks to Explore a Structural Definition of Place”, documento presentado en The New Methodologies for the Social Sciences Conference, University of Colorado, Boulder.

 

Hägerstrand, Torsten (1953), Innovation Diffusion as a Spatial Process, Chicago University Press, Chicago, Estados Unidos.

 

Hägerstrand, Torsten (1966), “Aspects of the Spatial Structure of Social Communication and the Diffusion of Information”, Papers and Proceedings in the Regional Science Association, 16, Regional Science Association International, pp. 27-42.

 

Hornsby, Katheleen (2003), “Spatial Diffusion: Conceptualizations and Formalizations”, documento de trabajo del National Center for Geographic Information and Analysis and the Department of Spatial Information Science and Engineering, University of Maine, http://www.spatial. maine.edu/~khornsby/KHI21.pdf>, 1 de junio de 2006.

 

Lesage, John (1998), Spatial Econometrics using matlab,  www.econ.utoledo.edu, 31 de mayo de 2006.

 

López, Santos (2003), “Empresarios e innovacion tecnológica en Sinaloa”, Región y Sociedad, 15(27), El Colegio de Sonora, México, pp. 179-214.

 

Malaver, Florentino y Marisela Vargas (2004), “Hacia una caracterización de los procesos de innovación en la industria colombiana: los resultados de un estudio de casos”, Academia, Revista Latinoamericana de Administración, 33, Consejo Latinoamericano de Escuela de Administración (cladea), Bogotá, Colombia, pp. 5-33.

 

Mandel, Ernest (1986), Los ciclos largos del capitalismo, Siglo XXI, México.

 

Méndez, Ricardo (2002), “Innovación y desarrollo territorial: algunos debates teóricos recientes”, eure, Revista Latinoamericana de Estudios Urbano Regionales, 28(84), Pontificia Universidad Católica de Chile, Santiago de Chile, pp. 63-84.

 

Morales, Elda y Carlos Vilalta (2007), “Una revisión de lo que se conoce de la economía basada en el conocimiento y sobre lo que indican los indicadores de innovación tecnológica”, inédito.

 

Myrdal, Gunnar (1957), Economic Theory and the Underdeveloped Regions, Duckworth, Londres, Inglaterra.

 

Ohmae, Kenichi (1997), El fin de Estado-nación. El ascenso de las economías regionales, Andrés Bello, Barcelona, España.

 

Perroux, François (1950), “Les espaces économiques”, Economie appliquée, 1, Bulletin de l’Institut de Science Économique Appliquée, Paris, pp. 225-244.

 

Rogers, Everett (1962), Diffusion of Innovations, The Free Press, Nueva York, Estados Unidos.

 

Rózga, Ryszard-Luter (2003), “Sistemas regionales de innovación. Antecedentes, origen y perspectivas”, Convergencia, 33, Universidad Autónoma del Estado de México, México, pp. 225-248.

 

Siebert, Horst (1969), Regional economic growth: theory and policy, International Textbook Company, Pensilvania, Estados Unidos.

 

Storper, Michael (1997), The Regional World: Territorial Development in a Global Economy, Guildford Press, Nueva York, Estados Unidos.

 

Schumpeter, Joseph (1939), Business Cycles: a theoretical and statistical analysis of the capitalist process, McGraw Hill, Nueva York-Londres.

 

Tobler, Waldo (1970), “A Computer Movie Simulation Urban Growth in the Detroit Region”, Economic Geography, 46(2), International Geographical Union, Commission on Quantitative Methods, pp. 234-240.

 

Torres, Arturo y Javier Jasso (2003), “Adquisiciones y funciones transfronterizas. El aprendizaje de los grupos corporativos mexicanos”, Seminario altec, Conocimiento, innovación y competitividad. Los desafíos de la globalización, México.

 

Urry, John (1996), “How Societies Remember the Past”, en Sharon Macdonald y Gordon Fyfe (eds.), Theorizing Museums, Blackwell, Oxford.

 

Vilalta-y Perdomo, Carlos (2003a), “Perspectivas geográficas en la sociología urbana: la difusión espacial de las preferencias electorales y la importancia del contexto local”, Estudios Demográficos y Urbanos, 18(3), El Colegio de México, México, pp. 147-177.

 

Vilalta-y Perdomo, Carlos (2003b), “Una aplicación del análisis espacial al estudio de las diferencias regionales del ingreso en México”, Economía, Sociedad y Territorio, 4(14), El Colegio Mexiquense, México, pp. 317-340.

 

Vilalta-y Perdomo, Carlos (2006), “Sobre la espacialidad de los procesos electorales urbanos y una comparación entre las técnicas de regresión ols y sam”, Estudios Demográficos y Urbanos, 21(1), El Colegio de México, México, pp. 83-122.

 

Vilalta-y Perdomo, Carlos (2007), ¿Se pueden predecir geográficamente los resultados electorales?: una aplicación del análisis de clusters y outliers espaciales”, Política y Gobierno, cide, en dictamen.

 

Weber, Alfred (1929), Theory of Location of Industries, Chicago University Press, Chicago.

 

 

Recibido: 15 de junio de 2006.

Aceptado: 28 de mayo de 2007.

 

Carlos J. Vilalta y Perdomo. Es doctor en estudios urbanos por The Portland State University y maestro en estudios urbanos por el Colegio de México. Es director de la División de Administración y Ciencias Sociales en el Tecnológico de Monterrey, Campus Santa Fe; candidato a investigador nacional en el sni desde 2004; actualmente es investigador visitante en la University of North Carolina en Chapel Hill. Su línea de investigación actual es: geografía electoral y metodología política. Entre sus publicaciones más recientes se encuentran: “Sobre la espacialidad de los procesos electorales urbanos y una comparación entre las técnicas de regresión ols y sam”, Estudios Demográficos y Urbanos, 21(1), El Colegio de México, México, pp. 83-122 (2006); en coautoría, “Una metodología formal para calcular el peso que los electores le dan a los elementos de evaluación ideológica”, Política y Gobierno, 13(1), cide, México, pp. 99-147 (2006); “Cómo enseñar autocorrelación espacial”, Economía, Sociedad y Territorio, 5(18), El Colegio Mexiquense, México, pp. 323-333 (2005).

 

Humberto Banda Ortiz. Es doctor en economía financiera por esade, Barcelona, y maestro en dirección de empresas por el ipade. Actualmente es profesor-investigador del Departamento de Administración y Finanzas en el itesm, Campus Santa Fe; profesor visitante de mit Sloan School of Management; candidato a investigador nacional en el sni desde 2005; profesor visitante de esade. Ha colaborado en diferentes organizaciones entre las que se incluyen ibm, Avon, Gas of France y Fleishman Hillard en las áreas de estrategia y finanzas. Su línea de investigación actual es: juegos globales aplicados a las crisis financieras. Entre sus publicaciones más recientes se encuentran: en coautoría, El capital de trabajo: modelos y decisiones financieras, impc, México, (2004); en coautoría, “Deuda externa y crisis: una visión política-económica”, Foro Internacional, 181, El Colegio de México, México, pp. 120-143 (2005); “Modelos teóricos de crisis de tipo de cambio y su aplicación a la crisis mexicana de 1994”, Revista Mexicana de Economía y Finanzas, 3(2), México, pp. 127-143 (2004).