Difusión tecnológica y convergencia económica: un análisis de las regiones y los sectores productivos españoles

 

Mª Jesús Delgado Rodríguez*

Inmaculada Álvarez Ayuso**

 

Abstract

 

This work analyses the regional and sectorial convergence in the Spanish economy in order to understand the role of the main tools used to decrease economic disparities. The novel techniques used here have provided us with important information about this process, as well as about the evolution of the productive efficiency of the Spanish economic sectors. We have used parametric stochastic frontier approach to estimate the technical efficiency of the Spanish productive sectors and to approximate the technological diffusion they have experienced. The conclusions stand out due to their implications in the choice of destinations for public expenditures.

 

Keywords: technical efficiency, public capital, regional convergence.

 

Resumen

 

Este trabajo analiza la convergencia regional y sectorial en la economía española con objeto de profundizar en el papel de los principales instrumentos utilizados para disminuir las disparidades económicas. Las técnicas empleadas son novedosas y permitieron obtener información relevante acerca de este proceso y la evolución de la eficiencia productiva de los sectores económicos españoles. Para ello, se utilizaron los desarrollos de la aproximación paramétrica de la frontera estocástica, lo que hizo posible estimar la eficiencia técnica de los sectores productivos españoles y la aproximación a la difusión tecnológica que experimentaron. Las conclusiones sobresalen por sus implicaciones en la selección del destino del gasto público.

 

Palabras clave: eficiencia técnica, capital público, convergencia regional.

 

 

* Facultad de Ciencias Jurídicas y Sociales, Universidad Rey Juan Carlos. Correo-e: mdelgado@fcjs.urjc.es.

** Facultad de Ciencias Económicas y Empresariales, Universidad Autónoma de Madrid. Correo-e: eccuay6@sis.ucm.es.

 

 

Introducción

 

La reducción de las desigualdades entre regiones y países constituye un objetivo que gana protagonismo progresivamente en los países miembros de la Unión Europea. Las dificultades de que estas economías converjan promueven investigaciones para establecer los instrumentos más eficaces que logren mayor paridad.[1] Durante los años ochenta y noventa las diferencias regionales en la Unión Europea no mostraron tendencias a la reducción, al contrario, aumentaron, mientras que la dispersión entre países disminuyó (Magrini, 1999; López-Bazo et al., 1999 y Giannetti, 2002).

Entre los mecanismos de convergencia considerados habitualmente se encuentra la difusión de tecnología que recoge la transmisión de ideas y técnicas de producción entre regiones y países. Una vía para generar convergencia en la renta es permitir que el nivel de tecnología de las economías de menores rentas alcance a las de rentas mayores; si existe un proceso de difusión tecnológica, las economías atrasadas disfrutarán la ventaja de adoptar a bajo coste las tecnologías empleadas en las más avanzadas.[2]

En esta investigación tratará de contrastarse la existencia de un efecto catch-up tecnológico entre las regiones españolas a partir de la aproximación que ofrece el concepto de eficiencia técnica; de modo que las mejoras en la eficiencia de un país estarán ligadas a su aproximación a la frontera eficiente y, por lo tanto, a la asimilación de tecnología.[3] La hipótesis del catch-up en términos de la convergencia en eficiencia permitirá comprobar si el proceso de integración favoreció el acceso de las regiones más atrasadas a nuevas tecnologías, en un mercado donde los intercambios entre ellas son muy intensos.

En este trabajo se emplearán técnicas frontera, que destacarán la medición de eficiencia técnica de cada uno de los sectores regionales: agricultura, industria, energía, construcción y servicios destinados a la venta en el periodo 1980-1995. Tratará de establecerse si los equipamientos de infraestructuras influyeron en el proceso de convergencia en eficiencia en esos años. Para llevar a cabo estos objetivos, se aplicarán los desarrollos para la estimación de fronteras de producción estocástica recogidos en Battese y Coelli (1995).

La literatura económica brinda numerosos trabajos que calculan funciones frontera en el análisis de la eficiencia (Färe et al.,1994; Fecher y Perelman,1992). En ellos se realizan comparaciones entre países y regiones, y entre agregados nacionales y sectoriales. La estimación de la eficiencia técnica en la economía española fue objeto de atención en investigaciones recientes: Gumbau (1998), Maudos, Pastor y Serrano (2000), entre otros, en las que se comprueban las desigualdades regionales y sectoriales existentes.

La actividad productiva de las regiones españolas se desarrolla en un marco de integración económica y monetaria que obliga a las empresas a realizar esfuerzos para reducir los niveles de ineficiencia en el uso de los factores productivos y aumentar su competitividad. En tal contexto, los resultados de esta investigación cobran interés por sus implicaciones al seleccionar el destino del gasto público, ya que el incremento de las infraestructuras es una posible vía para la obtención de mejores resultados.

La estructura del trabajo es la siguiente: el apartado uno describe las políticas principales y líneas de actuación de la economía española que atendió a las orientaciones de la Unión Europea. En el apartado dos se recogen las novedades metodológicas aportadas por el modelo de Battese y Coelli (1995) en la medición de la eficiencia, lo que permitió el establecimiento de las diferencias sectoriales y regionales existentes. A continuación, el apartado tres analiza la convergencia en eficiencia que hay entre las regiones españolas y trata de establecer el papel desempeñado por las dotaciones de infraestructura regional. Finalmente, se reseñan las conclusiones principales de este trabajo.

 

1. Las regiones españolas en la Unión Europea. Políticas principales y líneas de actuación para la convergencia

 

La solidaridad entre las regiones de la Unión Europea, el progreso económico y social y el refuerzo de la cohesión forman parte de los objetivos globales de la comunidad para aminorar las disparidades en los niveles de desarrollo de las diversas regiones, como se establece en el tratado constitutivo de las comunidades europeas. Los instrumentos de solidaridad, los fondos estructurales y el fondo de cohesión absorben cerca de un tercio del presupuesto de la Unión Europea (cerca de 36,000 millones de euros en 2004). Los recursos se distribuyen mediante programas de desarrollo plurianuales gestionados de manera conjunta por los Estados miembros, las regiones y la comisión europea.

Las prioridades de la Unión Europea para alcanzar la convergencia regional son las siguientes:

 

·       Apoyo para la generación de empleos y el crecimiento de los Estados miembros y las regiones menos desarrolladas. Este objetivo implicó que las regiones con producto nacional per cápita inferior a 75% del promedio europeo recibieron ayudas europeas mediante los fondos estructurales.

·       La Unión Europea trata de modernizar y diversificar la estructura económica regional con la ampliación y mejora de las infraestructuras básicas, también busca la protección del ambiente, el refuerzo de la capacidad administrativa, la mejora de las instituciones del mercado laboral, los sistemas de educación y formación, porque con esto aumenta el capital humano. Además, los Estados miembros cuyo producto nacional esté por debajo del 90% del promedio de la comunidad serán elegibles para el Fondo de Cohesión, con ello continuará el financiamiento de los programas de transporte y ambiente.

·       Fomento a la competitividad regional y el cambio estructural: el objetivo es promover, mediante programas regionales, el cambio económico en las zonas industriales, urbanas y rurales con el refuerzo de su competitividad y capacidad de atracción teniendo en cuenta las disparidades económicas, sociales y territoriales existentes. Además, los programas nacionales ayudarían a la población a anticipar y adaptarse al cambio económico, y así ajustarse a las prioridades de políticas de la Estrategia Europea de Empleo.

·       Fomento del desarrollo armonioso y equilibrado del territorio de la unión. Todas las regiones limítrofes con las fronteras exteriores e inferiores, tanto terrestres como marítimas, estarían incluidas en la cooperación transfronteriza. Se trata, principalmente, de plantear soluciones conjuntas a problemas comunes entre autoridades vecinas, por ejemplo: el desarrollo urbano, rural y costero, y el establecimiento de redes de pequeñas y medianas empresas.

 

Este trabajo se centra en las regiones españolas y el desarrollo de la convergencia en el territorio nacional. El Estado español se compone de 17 Comunidades Autónomas o regiones: Asturias, Galicia, Cantabria, Aragón, Cataluña, Canarias, Extremadura, La Rioja, Castilla La Mancha, Baleares, Castilla León, Andalucía, Madrid, Navarra, País Vasco, Murcia y Valencia (véase mapa i).

 

Mapa i

Las regiones españolas

 

 

2. Enfoque metodológico

 

Este trabajo utiliza una metodología novedosa: las técnicas frontera que permiten medir la ineficiencia de una economía y que permitirán ofrecer mayor información acerca del proceso productivo de la economía española. Este es el punto de partida para el análisis de convergencia, que centraremos en el caso español, con el fin de aplicar esta metodología en un estudio e ilustrar esta técnica. El estudio de la ineficiencia de una economía puede realizarse a partir de dos enfoques, que se diferencian en los supuestos asignados a los datos. El primero es el no paramétrico, que requiere imponer una determinada relación funcional entre las variables; el que comúnmente se usa es el análisis de envolvente de datos (data envelopment analysis, dea). Un resumen de estas técnicas está en Maudos, Pastor y Serrano (2000).

El segundo enfoque es el paramétrico de la frontera estocástica, que permite estimar las elasticidades de los factores de la función de producción por ser necesario aplicar una forma funcional específica. Este enfoque admite diferentes especificaciones de acuerdo con la tecnología adoptada en la estimación de la función de producción. Los desarrollos de estos modelos están en Battese y Coelli (1995).

A continuación se presenta el modelo empleado para medir la eficiencia de los sectores regionales de la economía española y los resultados obtenidos para el periodo 1980-1995.

 

2.1. Método de estimación

 

En este trabajo se utiliza la aproximación paramétrica de la función estocástica; esto implica estimar una función de producción frontera en la que la desviación entre el nivel de output observado y el máximo posible abarca dos componentes: un término de error, v_i, que capta el efecto de variables que no están bajo el control de la unidad productiva analizada, y un término de ineficiencia, u_i. El modelo de frontera de producción estocástica, que abajo se expone, fue propuesto de forma simultánea por Aigner, Lovell y Schimdt (1977) y Meeusen y Van den Broeck (1977).

 

                   Y_i = f(X_i,b) +e_i,

i=1, …, N

                   _i = v_i + u_i               u_i £ 0

 

A partir de este esquema se plantean diferentes modelos, entre los que destaca el desarrollado por Battese y Coelli (1995), utilizado en este trabajo, que contribuye de manera importante a la flexibilización del supuesto de invarianza de la eficiencia en el tiempo, porque brinda la posibilidad de introducirlo como un regresor en la ecuación correspondiente a la ineficiencia. El modelo es aplicable a estudios en los que se dispone de un panel de datos y las eficiencias técnicas de las regiones varían en el tiempo, como es el caso que se expone en este artículo.

Como plantean Battese y Coelli (1995), se considerará la función de producción estocástica en un panel de datos:

 

Y_it = exp(X_itb + v_it – u_it)                                                       (1)

t = 1,…, T

i = 1,…, N

 

Donde Y_it es la producción en el periodo t-ésimo y para la i-ésima región, X_it un vector (1 × k) de variables explicativas y b un vector (k × 1) de parámetros desconocidos; v_it representa los errores aleatorios independientes e idénticamente distribuidos como una normal con media cero y varianza s²_v, e independientemente distribuidos de u_it. Por su parte, u_it está compuesta por variables aleatorias nonegativas, asociadas a la ineficiencia técnica en producción y obtenidas a partir de la distribución normal truncada[4] en cero con media Z_itd y varianza s². Z_it es un vector (1 × m) de variables explicativas asociadas a la ineficiencia técnica en el tiempo y d es vector (m × 1) de coeficientes desconocidos.

La ecuación (1) especifica la frontera estocástica en términos de los valores de producción originales. Mientras que la ineficiencia técnica, u_it, es función de un conjunto de variables explicativas, Z_it, y un vector de coeficientes desconocidos, d.

De este modo la ineficiencia técnica se expresa como:

 

U_it = Z_itd + W_it                                                                                   (2)

 

Donde W_it sigue una distribución normal truncada en –Z_itd con media cero y varianza s².

Las ecuaciones (1) y (2) se estiman con el método de máxima verosimilitud[5] y se aplican ecuaciones simultáneas, así se obtiene la eficiencia técnica de la siguiente forma:

 

Te_it = exp(–u_it) = exp (– Z_itd – W_it)                           (3)

 

En los trabajos realizados pueden encontrarse otras opciones para flexibilizar el supuesto restrictivo de la invarianza de la eficiencia en el tiempo. Este era un supuesto frecuente en los primeros análisis, por lo que no era necesario asumir ningún supuesto distribucional para los términos de ineficiencia y de error. En este caso, se parte de la frontera estocástica:

 

t = 1,…, T

i = 1,…, N

 

Se supone que la ineficiencia es constante en el tiempo; entonces u_i podría definirse como , lo que permitiría llevar a cabo las estimaciones mediante los modelos estándar de datos de panel (estimación por efectos fijos).

 

t = 1,…, T                         

i = 1,…, N

 

Frente a esta situación, los trabajos más recientes flexibilizan el supuesto de invarianza en el término de ineficiencia. Para ello se plantean dos alternativas. Por un lado, se suponen sendas distribuciones para los términos error e ineficiencia, lo que llevaría al cálculo de la última utilizando la distribución condicionada al término de error compuesto: E(u_i/e_i), como plantean Gumbau (1998) y Gumbau y Maudos (1996).

Por otra parte, y como resulta más razonable cuando se dispone de un panel de datos, también se propone la posibilidad de continuar con la introducción del término de ineficiencia como si se tratase de los efectos fijos o aleatorios correspondientes al modelo de datos del panel, aunque suponiendo que éste es función del tiempo. Sin embargo, la limitación que presenta esta alternativa se encuentra en la imposición de una estructura demasiado rígida en el tipo de variación del término de ineficiencia. Esta es la opción adoptada por Pedraja et al. (1999), que en su trabajo permiten que la ineficiencia varíe en el tiempo y asumen que los efectos fijos sean función lineal de éste. Dicha opción es similar a la planteada en Battese y Coelli (1993), quienes proponen una forma exponencial del tiempo para el componente de ineficiencia: U_it = (U_iexp(–h(t–T)), lo cual implica que la ineficiencia crece, decrece o se mantiene constante, dependiendo del valor que adopte el parámetro h.

Por su parte, en el modelo de Battese y Coelli (1995), pese a presentar la ineficiencia en forma de efectos fijos, se flexibiliza la estructura del tipo de variación que sigue la ineficiencia, frente a otros trabajos e incluso en sus versiones anteriores (Battese y Coelli, 1993). Así pues, esta, en sí misma, constituye una función –ecuación (2)–, cuyos regresores se determinan en la investigación. De esta forma, las variables explicativas de dicha ecuación pueden ser las que incorporan la función de producción estocástica –ecuación (1)–, efectos fijos (individuales o temporales), así como cualquier variable que determine cambios en la ineficiencia.

Las medidas de eficiencia técnica relativa a la frontera de producción estocástica –ecuación (1)– se definen como:

 

ϕ _it= E(Y^*_it\U_it,X_it)/, E(Y^*_it\U_it=0,X_it) = exp(–u_it)                     (4)

 

Donde Y^*_it es la producción en t de la i-ésima región, que será igual a exp(Y_it) puesto que la variable dependiente será tomada en logaritmos. Por su parte, la eficiencia de la región i-ésima en t, ϕ_it, alcanzará valores entre cero y uno, este último es el caso más favorable.

 

2.2. Análisis de la eficiencia sectorial en las regiones españolas

 

El análisis de la eficiencia mediante el enfoque de frontera estocástica parte del cálculo de la frontera de producción estocástica. Para ello, y como en la mayor parte de los estudios empíricos realizados, se supone que la tecnología subyacente a la función de producción es del tipo Cobb-Douglas, en la que se incluyen los inputs privados (stock de capital privado y empleo). De esta manera, la forma funcional que representará la producción sectorial y nacional para cada una de las regiones españolas será la siguiente:

 

 

r = 1,…, S; i = 1,…, I y t = 1,…, T                         (5)

 

Donde los subíndices hacen referencia al sector productivo (r y s), a la Comunidad Autónoma (i) y la fracción del tiempo (t), y Y_ri(t) es el valor de la producción privada (vabpm), en pesetas constantes de 1990 (excluida la producción de los servicios no destinados a la venta).

L_ri(t) representa el empleo del sector privado (excluido el empleo del sector servicios no destinado a la venta).

KPRIV_ri(t) es el valor del stock de capital privado productivo (sin el stock de capital residencial), a precios constantes de 1990.

D_r significa una variable dummy sectorial que toma el valor 1 cuando r = s, y 0 en caso contrario.

Siguiendo la especificación expuesta en la ecuación (2), el término de ineficiencia técnica se explica por un término independiente y dos variables explicativas, Z₁ y Z₂, que representan una tendencia temporal y una variable regional respectivamente.

En cuanto a la información estadística utilizada, las series de producción y empleo proceden de Cordero y Gayoso (1996), elaboradas con base en las cifras de la Contabilidad Regional de España y publicadas por el Instituto Nacional de Estadísticas (ine). Las series de capital privado proceden de la publicación de la Fundación bbva, y contienen una evaluación a escala regional del stock de capital privado para los sectores de la economía española.

En este documento, la eficiencia productiva se calculó como el ratio entre la producción media y la máxima posible mediante la utilización de los inputs eficientemente.[6] El cuadro 1 presenta los resultados obtenidos con el uso de la expresión o ecuación (4), que indica: si el valor es igual a 1, entonces la región es eficiente, y lo es menos cuanto menor sea el valor obtenido. De manera paralela: (1-ϕ_it)*100 mostraría el porcentaje en que podría incrementarse el valor añadido bruto (vab) de las regiones sin necesidad de aumentar los inputs utilizados. Se escogieron los años 1980, 1985, 1990 y 1995 para recoger la evolución de la eficiencia en ese periodo.

Las técnicas empleadas permiten extraer información no habitual en los estudios económicos; consisten en la medición del grado de ineficiencia de esos sectores productivos. Al comparar los resultados se comprueba la existencia de desigualdades regionales y sectoriales, al igual que en otros trabajos realizados para la economía española (Gumbau y Maudos, 1996; Maudos, Pastor y Serrano, 2000). En cuanto a su evolución, destacan las mejoras en la eficiencia en las regiones en los años estudiados. Para el total de la economía, las regiones más eficientes fueron Madrid, Cataluña, La Rioja y Baleares; entre las menos eficientes estuvieron Asturias, Extremadura, Castilla la Mancha, Castilla León y Galicia.

En la escala sectorial se observa que industria, construcción y servicios destinados a la venta obtienen mayores niveles de eficiencia que los sectores de agricultura y energía. En el primero todas las regiones se sitúan muy lejos de la frontera, aunque su evolución es favorable, con excepción de Aragón, Castilla La Mancha y Valencia. Las regiones de Andalucía, Baleares y País Vasco están entre las más eficientes en los años estudiados, mientras que Extremadura y Madrid podrían aumentar su producción si el uso de los factores productivos es más eficiente.

Para el sector energético los niveles de eficiencia fueron menores, aunque los avances en el periodo son considerables. Entre las regiones más eficientes de la fase se encuentran País Vasco, Cataluña, Andalucía y Murcia; entre las menos, Aragón y Cantabria.

 

Cuadro 1

Eficiencias sectoriales por ccaa, de acuerdo con el modelo de Battese y Coelli

SECTOR	Total				Agricultura					Energía				Industria				Construcción				Servicios D.V.
REGIÓ N	1980	1985	1990	1995	1980	1985		1990	1995	1980	1985	1990	1995	1980	1985	1990	1995	1980	1985	1990	1995	1980	1985	1990	1995
Andalucía	0.867	0.882	0.874	0.839	0.365	0.412	0.431		0.413	0.695	0.626	0.720	0.776	0.887	0.937	0.939	0.953	0.948	0.979	0.983	0.982	0.970	0.977	0.978	0.980
Aragón	0.829	0.828	0.843	0.824	0.327	0.324	0.312		0.307	0.530	0.555	0.531	0.548	0.829	0.907	0.941	0.957	0.897	0.948	0.972	0.979	0.975	0.983	0.985	0.986
Asturias	0.802	0.812	0.795	0.792	0.272	0.271	0.289		0.293	0.475	0.464	0.445	0.461	0.862	0.904	0.909	0.951	0.963	0.981	0.985	0.986	0.971	0.978	0.979	0.984
Baleares	0.884	0.910	0.879	0.872	0.287	0.317	0.318		0.356	0.483	0.467	0.558	0.534	0.834	0.877	0.853	0.903	0.899	0.985	0.958	0.966	0.986	0.986	0.986	0.988
Canarias	0.908	0.964	0.928	0.893	0.353	0.369	0.405		0.358	0.526	0.570	0.689	0.683	0.881	0.896	0.949	0.944	0.903	0.970	0.975	0.974	0.975	0.986	0.984	0.985
Cantabria	0.761	0.792	0.825	0.830	0.270	0.283	0.345		0.356	0.383	0.343	0.455	0.459	0.844	0.896	0.924	0.967	0.898	0.939	0.972	0.969	0.974	0.984	0.985	0.986
Castilla y León	0.827	0.801	0.789	0.774	0.299	0.324	0.322		0.366	0.488	0.518	0.531	0.555	0.898	0.923	0.938	0.969	0.899	0.961	0.965	0.969	0.975	0.971	0.973	0.977
Castilla la M.	0.821	0.798	0.807	0.765	0.357	0.363	0.361		0.342	0.715	0.679	0.785	0.874	0.825	0.869	0.927	0.927	0.934	0.975	0.962	0.962	0.967	0.970	0.978	0.977
Cataluña	0.886	0.887	0.890	0.853	0.354	0.332	0.369		0.361	0.597	0.580	0.640	0.680	0.885	0.929	0.945	0.965	0.934	0.950	0.979	0.981	0.976	0.983	0.986	0.986
Extremadura	0.792	0.786	0.798	0.775	0.299	0.330	0.352		0.306	0.407	0.747	0.705	0.700	0.794	0.831	0.833	0.857	0.909	0.982	0.967	0.974	0.963	0.956	0.966	0.973
Galicia	0.839	0.799	0.790	0.770	0.301	0.297	0.312		0.303	0.676	0.699	0.696	0.748	0.853	0.901	0.920	0.953	0.907	0.966	0.971	0.963	0.975	0.971	0.967	0.978
Madrid	0.942	0.949	0.946	0.900	0.317	0.290	0.283		0.282	0.466	0.557	0.602	0.579	0.903	0.942	0.966	0.977	0.896	0.956	0.977	0.982	0.984	0.987	0.988	0.989
Murcia	0.938	0.920	0.914	0.869	0.343	0.374	0.445		0.397	0.903	0.727	0.880	0.925	0.834	0.846	0.869	0.924	0.951	0.977	0.977	0.976	0.978	0.983	0.981	0.979
Navarra	0.867	0.870	0.878	0.849	0.342	0.336	0.359		0.353	0.410	0.557	0.588	0.563	0.894	0.909	0.951	0.967	0.935	0.986	0.964	0.968	0.979	0.983	0.986	0.985
Rioja	0.929	0.977	0.915	0.956	0.298	0.379	0.382		0.381	0.470	0.656	0.748	0.660	0.965	0.982	0.977	0.988	0.963	0.982	0.977	0.965	0.985	0.983	0.985	0.987
Valencia	0.910	0.916	0.877	0.848	0.351	0.334	0.362		0.334	0.626	0.697	0.727	0.778	0.864	0.914	0.909	0.940	0.955	0.983	0.975	0.974	0.977	0.982	0.982	0.982
País Vasco	0.830	0.855	0.857	0.850	0.341	0.376	0.412		0.404	0.685	0.681	0.804	0.906	0.868	0.891	0.931	0.967	0.921	0.979	0.982	0.977	0.983	0.987	0.988	0.987

Fuente: Elaboración propia a partir de las series procedentes de Cordero y Gayoso (1996) y Fundación bbva (1998).

 

 

Las regiones más eficientes en el sector industrial son Cataluña, Madrid y La Rioja; y las menos, Extremadura, Castilla La Mancha, Canarias y Murcia. En el sector de construcción, las regiones más eficientes son Madrid, Cataluña, Andalucía y Asturias, mientras que La Rioja, Castilla La Mancha, Baleares y Galicia son las menos eficientes, y no existen grandes diferencias en los niveles de eficiencia entre las regiones.

El sector servicios destinados a la venta presenta las diferencias menores entre los niveles de eficiencia regionales. Madrid, Baleares, Cataluña y La Rioja mostraron proporciones elevadas, mientras que Extremadura, Murcia, Castilla León, Castilla La Mancha y Galicia tienen niveles de eficiencia inferiores.

La disponibilidad de datos sectoriales y regionales para la economía española proporciona un panorama amplio del esquema productivo español. El diseño de políticas económicas encaminadas a favorecer la eficiencia productiva constituyen, por lo tanto, una importante fuente de crecimiento para la economía.

 

3. Convergencia en eficiencia de las regiones españolas

 

Los contrastes en la eficiencia con que actúan los sectores productivos regionales muestran el incremento potencial de la producción que las regiones españolas podrían lograr si eliminaran sus niveles de ineficiencia en el empleo de los factores de producción privados, capital y trabajo. Estos niveles pueden verse condicionados por factores exógenos, sobre los que las regiones tienen un reducido margen de maniobra, este es el caso de los equipamientos de infraestructura. Con el objeto de analizar si las regiones se aproximan a sus niveles de eficiencia y tratar de determinar si el capital público influye favorablemente en este proceso, se investigó la convergencia en el ámbito sectorial y, para el total de la economía, los niveles de eficiencia. En este apartado se utilizó la valoración del stock regional elaborada por Álvarez y Delgado (1999 y 2000), donde se recogió la capacidad de los equipamientos de infraestructura con los que cuenta cada región en unidades físicas.

Esta es una cuestión de gran importancia para interpretar las diferencias en el crecimiento de las regiones españolas y comprobar en qué medida el marco de integración logrado en el seno de la Unión Europea durante el periodo analizado favoreció la convergencia en la economía española. El proceso de acercamiento tecnológico dista mucho de ser automático y dependerá de la capacidad del país para incorporar tecnologías avanzadas y adaptarlas a sus procesos productivos. La existencia de convergencia condicional daría pie a que cada territorio tendiese a convergir a su propio modo estacionario, y podrían ser muy distintos entre sí. Por lo tanto, podrían mantenerse disparidades importantes debidas a la persistencia en sus posiciones relativas. Tal situación justificaría el mantenimiento de una política regional, que debería intentar corregir los factores responsables de las diferencias en el largo plazo.

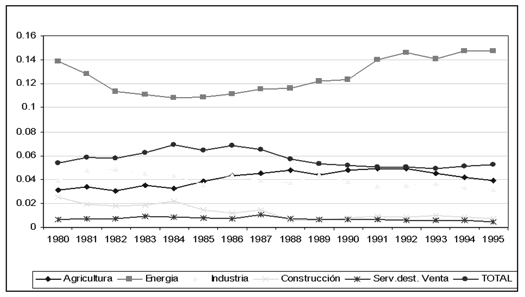
En primer lugar, se estudió la sigma convergencia que permite obtener información acerca de la disminución en las desigualdades entre regiones en el transcurso del tiempo. La gráfica i ilustra los resultados obtenidos y la evolución de la desviación típica del indicador de eficiencia. Los sectores que registran una evolución más desfavorable, o que aumenta las desigualdades regionales en este periodo, son los de energía y agricultura (en los últimos tres años mejora su evolución, pero no logra alcanzar los niveles obtenidos a comienzo del periodo), asimismo, tuvieron menores niveles de eficiencia. Construcción e industria muestran trayectorias más favorables y, por lo tanto, disminuyen las diferencias regionales, si bien este proceso no es constante en el tiempo. El sector de servicios destinados a la venta es el que mantiene una evolución más homogénea en todo el periodo. Para el total de la economía, el estudio de la sigma convergencia muestra cómo las desigualdades regionales se redujeron ligeramente en el periodo analizado. Estos resultados están en línea junto con los obtenidos en otros trabajos para la economía española (Maudos, Pastor y Serrano, 2000).

 

Gráfica i

Sigma convergencia en eficiencia

 

 

A continuación, este trabajo se centra en el estudio de la convergencia beta no condicionada. En este caso, se analiza si aquellas regiones con menores niveles iniciales de eficiencia experimentan mayores ganancias. Para ello, debe estimarse la siguiente ecuación:

 

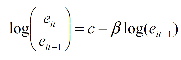                                                                                       (6)

                                                                                        

 

Donde e_it representa la observación t-ésima para la eficiencia correspondiente a la región i-ésima. Cuando la relación entre el crecimiento de la eficiencia  y el nivel inicial de la misma es inversa y significativa, se produce un proceso de “convergencia” entre regiones (Barro y Sala-i-Martin, 1992).

El cuadro 2.1 recoge los resultados de este análisis.[7] Puesto que se dispone de un panel de datos, debe determinarse cuál de los posibles estimadores es el adecuado. El test de Hausman corrobora la existencia de efectos fijos, lo que lleva a presentar el estimador en desviaciones ortogonales. Sin embargo, puesto que el modelo es dinámico, ya que el regresor es la propia variable dependiente en el periodo inicial, la variable explicativa es estocástica. Por este motivo, se aplican variables instrumentales en el estimador en desviaciones ortogonales debido a la endogeneidad del regresor (el instrumento viene de la variable explicativa retardada en dos periodos). Además, los residuos no presentan problemas de autocorrelación, como se observa en el contraste efectuado, y sus errores estándar de heteroscedasticidad han sido corregidos. Cuando el signo de la pendiente es negativo en la ecuación (6), indica un acercamiento de las regiones menos eficientes con las que lo son más. Según esto, el análisis realizado permite corroborar dicha convergencia entre regiones durante el periodo considerado. Por sectores, la significatividad de los coeficientes corrobora esta tendencia, salvo para el de energía.

Por último, se estudia la influencia de las infraestructuras productivas en este proceso, para ello se analiza la convergencia condicionada. Se trata de determinar si la convergencia en los niveles de eficiencia está condicionada por estos equipamientos, de manera que el aumento de las infraestructuras regionales sería una vía para disminuir la discrepancias en eficiencia.

A continuación, se introduce la variable de infraestructuras como regresor adicional en la ecuación de convergencia (6), derivada a partir del Modelo Neoclásico, lo que ha permitido el análisis de la influencia que ejercen dichos equipamientos en el proceso de convergencia. Tras recurrir al mismo método de estimación utilizado en el estudio de la ecuación (6), se incorpora el indicador de infraestructuras totales en el cuadro 2.2. Se observa una mejora sustancial en la velocidad de acercamiento en niveles de eficiencia para el total de la economía, dado que el coeficiente β continúa siendo negativo y además aumenta su cuantía. A escala sectorial sucede lo mismo en servicios destinados a la venta e industria. Por su parte, el sector de la construcción se mantiene estable, mientras que se comprueba la dificultad de lograr mejoras de eficiencia en el sector agrario. En cuanto al sector energético se ratifica cómo la introducción del capital público afecta de manera negativa su proceso de convergencia, lo que puede estar relacionado nuevamente con las dificultades de medición de su stock.

 

Cuadro 2.1

Convergencia β en niveles de eficiencia

 

Cuadro 2.2

Convergencia β condicional en niveles de eficiencia

 

 

Conclusiones

 

El desarrollo de técnicas que permiten obtener mayor información acerca del comportamiento de las economías supone avances significativos en la comprensión de los mecanismos de crecimiento y convergencia entre economías. En este trabajo se utilizaron técnicas de frontera que hacen viable la medición de la eficiencia técnica a escala regional y sectorial en la economía española para el lapso 1980-1995. El empleo de esta metodología detectó los problemas relacionados con el uso eficiente de los factores productivos, lo que contribuye a la orientación del diseño de medidas necesarias de política económica. La aplicación de estas técnicas para el caso español muestra que tras la incorporación de España a la Unión Europea la eficiencia técnica de los sectores productivos españoles experimentó una evolución favorable. Estos incrementos contribuyeron al crecimiento de los sectores productivos regionales.

El análisis de convergencia en eficiencia comprobó que el mayor aumento se produjo en las regiones que partían de niveles de eficiencia menores; es el caso de Extremadura, Castilla La Mancha, Castilla León y Andalucía, lo que corrobora la influencia positiva de los equipamientos de infraestructura en este proceso, entre los que destacan los de comunicaciones. Estos resultados apoyan la inversión en infraestructura como vía para reducir los niveles de ineficiencia y lograr incrementos en la producción privada regional, y manifiesta el papel favorable que la política de inversión pública jugó en este periodo, lo que avala las políticas regionales que optan por impulsar la acumulación de este factor en regiones desfavorecidas como instrumento para reducir las disparidades regionales.

Las políticas regionales planteadas en Europa y España incluyeron las infraestructuras productivas como uno de los ejes de su actuación y se diseñaron intervenciones orientadas a impulsar el crecimiento económico de las regiones más atrasadas mediante la provisión de un nivel de infraestructura que garantice el establecimiento de condiciones mínimas adecuadas para el desarrollo de la actividad económica, con atención al impacto positivo en la localización y la eficiencia de los factores productivos privados.

 

Bibliografía

 

Abramovitz, Moses (1986), “Catching-Up, Forging Ahead and Falling Behind”, Journal of Economic History, 46: 86-125.

 

Aigner, Dennis J., C. A. Knox Lovell y Peter Schmidt (1977), “Formulation and Estimation of Stochastic Frontier Production Function Models”, Journal of Econometrics, 6: 21-37.

 

Álvarez, Inmaculada y M^a de Jesús Delgado (1999), Las infraestructuras productivas en España y su distribución regional: Una propuesta de estimación en unidades físicas, documento de trabajo, 0199, Instituto Universitario Ortega y Gasset, Fundación Ortega y Gasset, Madrid.

 

_____ (2000), “Las infraestructuras productivas en España: estimación del stock en unidades físicas y análisis de su impacto en la producción privada regional”, Revista Asturiana de Economía, 19: 155-181.

 

Arellano, Manuel y Stephen Bond (1988), Dynamic Panel Data Estimation Using dpd, documento de trabajo, 88/15, The Institute for Fiscal Studies, Londres.

 

Barro, Robert J. y Xavier Sala-i-Martin (1992), “Convergence”, Journal of Political Economy, 100 (2): 223-251.

 

Battese, Georges y Tim Coelli (1993), A Stochastic Frontier Production Function Incorporating a Model for Technical Inefficiency Effects, documento de trabajo, 69/93, Econometrics and Applied Statistics, Department of Econometrics, University of New England, Armidale.

 

_____ (1995), “A Model for Technical Inefficiency Effects in a Stochastic Frontier Production Function for Panel Data”, Empirical Economics, 20: 325-332.

 

Coelli, Tim (1996), A Guide to Frontier Version 4.1: A Computer Program for Stochastic Frontier Production and Cost Function Estimation, documento de trabajo cepa, 96/07, Centre for Efficiency and Productivity Analysis, University of New England, Armidale.

 

Cordero, Gervasio y Ángeles Gayoso (1996), El comportamiento de las economías regionales en tres ciclos de la economía española: primera explotación de una serie (1980-1995) del vab regional a precios constantes (base 1986), Contabilidad Regional de España, Dirección de Análisis y Programación Presupuestaria, Ministerio de Economía y Hacienda, Madrid.

 

De la Fuente, Ángel (2002), “On the Sources of Convergence: A Close Look at the Spanish Regions”, European Economic Review, 46: 569-599.

 

Färe, Rolf, Shawna Grosskopf, Mary Norris y Zhongyang Zhang (1994), “Productivity Growth, Technical Progress and Efficiency Change in Industrialized Countries”, American Economic Review, 84 (1): 66-83.

 

Fecher, Fabienne y Sergio Perelman (1992), “Productivity Growth and Technical Efficiency in oecd Industrial Activities”, en Richard E. Caves (ed.), Industrial Efficiency in Six Nations, The mit Press, pp. 459-488.

 

Fundación bbva (1998), El “stock” de capital en España y su distribución territorial, Bilbao.

 

Giannetti, Mariassunta (2002), “The Effects of Integration on Regional Disparities: Convergence, Divergence or Both?”, European Economic Review, 46 (3): 539-567.

 

Gumbau Albert, Mercedes (1998), “La eficiencia técnica de la industria española”, Revista Española de Economía, 5 (1): 67-84.

 

_____ y Joaquín Maudos (1996), “Eficiencia productiva sectorial en las regiones españolas: una aproximación frontera”, Revista Española de Economía, 13 (2): 239-260.

 

López Bazo, Enrique, Esther Vayá, Antonio J. Mora y Jordi Suriñach (1999), “Regional Economic Dynamics and Convergence in the European Union”, The Annals of Regional Science, (33) 3: 343-370.

 

Magrini, Stefano (1999), “The Evolution of Income Disparities Among the Regions of the European Union”, Regional Science and Urban Economics, (29) 2: 257-281.

 

Mankiw, N. George, David Romer y David N. Weil (1992), “A Contribution to the Empirics of Economics Growth”, Quarterly Journal of Economics, cvii (2): 407-437.

 

Maudos, Joaquín, José M. Pastor y Lorenzo Serrano (2000), “Crecimiento de la productividad y su descomposición en progreso técnico y cambio en la eficiencia: una aplicación sectorial y regional en España (1964-93)”, Investigaciones Económicas, 24 (1): 197-205.

 

Meeusen, Wim y Julien van den Broeck (1977), “Efficiency Estimation from Cobb-Douglas Production Functions with Composed Error”, International Economic Review, 18 (2): 435-444.

 

Paci, Raffaele y Francesco Pigliaru (2002), “Technological Diffusion, Spatial Spillovers and Regional Convergence in Europe”, en Juan Ramón Cuadrado Roura y Marti Parellada (eds.), Regional Convergence in the European Union. Facts, Prospects and Policies, Springer, Heildeberg.

 

Pedraja, Francisco, Julián Ramajo y Javier Salinas (1999), “Eficiencia productiva del sector industrial español: un análisis espacial y sectorial”, Papeles de Economía Española, 80: 51-67.

 

 

Enviado: 30 de mayo de 2004.

Reenviado: 2 de diciembre de 2004.

Aceptado: 8 de febrero de 2005.

 

Mª Jesús Delgado Rodríguez es doctora en ciencias económicas y empresariales por la Universidad Complutense. Labora para la Universidad Rey Juan Carlos en la Facultad de Ciencias Jurídicas y Sociales, campus de Vicálvaro.

 

Inmaculada Álvarez Ayuso es también doctora en ciencias económicas y empresariales por la Universidad Complutense. En el campus de Somosaguas de esta universidad se desempeña profesionalmente.

Las líneas de investigación de ambas versan sobre la eficiencia técnica, las políticas públicas en capital público y en educación, así como la convergencia regional. En cuanto a sus publicaciones conjuntas, se cuentan las siguientes: 1) “Infraestructuras y eficiencia técnica: un análisis a partir de técnicas frontera”, Revista de Economía Aplicada, 2003; 2) “Dinámica de los equipamientos de transporte, comunicaciones y energía de las regiones españolas”, Boletín ice Económico, núm. 27, 2002, pp. 9-17; 3) Estimación del capital público, capital privado y capital humano para la UE-15, documento de trabajo, Instituto de Estudios Fiscales, Madrid, 2002; 4) Medición de la eficiencia técnica para los países de la ue, documento de trabajo, Instituto Complutense de Análisis Económico, núm. 0210, Madrid, 2002; 5) “Medición de la eficiencia técnica en la economía española: el papel de las infraestructuras productivas”, Papeles de Trabajo, núm. 18/01, Instituto de Estudios Fiscales, Madrid, 2001; 6) “Metodología para la elaboración de índices de equipamientos de infraestructuras productivas”, revista Momento Económico, núm. 117, septiembre-octubre de 2001, pp. 20-35, y 7) “Evaluación de la eficiencia técnica en los países miembro de la Unión Europea”, Gestión y Política Pública, xiv (1), cide, México, primer semestre de 2005, pp. 107-128.