Cómo enseñar autocorrelación espacial

 

Carlos Javier Vilalta y Perdomo*

 

 

Abstract

 

This article discusses an exercise whose main aim is to teach spatial autocorrelation in an efficient manner to University students. We apply the basic concepts of dependency and spatial heterogeneity and include information about the usage of open source software to compute the spatial autocorrelation coefficients.

 

Keywords: education, statistics, spatial autocorrelation.

 

Resumen

 

Este artículo muestra un ejercicio cuyo objetivo es enseñar autocorrelación espacial de manera eficaz y eficiente a alumnos universitarios. Se explican los conceptos básicos de dependencia y heterogeneidad espaciales y se incluye información sobre el uso de software libre para el cómputo de coeficientes de autocorrelación espacial.

 

Palabras clave: educación, estadística, autocorrelación espacial.

 

 

* Instituto Tecnológico y de Estudios Superiores de Monterrey campus Ciudad de México. Correo-e: carlos.vilalta@itesm.mx.

 

 

1. Definición del problema: el alto precio de la complicación estadística

 

El número de estudiantes universitarios de las diversas disciplinas sociales y naturales interesados en aprender las técnicas del análisis espacial está aumentando.[1] Hay dos razones elementales para lo anterior: muchos están claramente conscientes de 1) la creciente importancia de los sistemas de información geográfica (sig) en las áreas de investigación, y 2) la necesidad que hay en el mercado laboral de analistas de datos entrenados en técnicas estadísticas complejas y novedosas.

También, y de manera constante, los profesores universitarios se mantienen al corriente de los avances metodológicos y los nuevos diseños y técnicas de investigación, a la par que incesantemente introducen innovaciones y mejoran sus cursos para lograr la mejor experiencia educativa posible.

Sin embargo, es muy común que estudiantes y docentes encuentren dificultades para lograr estos objetivos académicos. Uno de los mayores obstáculos en la enseñanza de la estadística espacial son, particularmente, los altos costos de la paquetería estadística para los sig.

Ahora bien, una práctica pedagógica común entre los profesores de estadística (y de otras materias) es la construcción del proceso de enseñanza-aprendizaje empezando por los conceptos y técnicas más simples hasta llegar a los más complicados, intuitivamente hablando. Simultáneamente, en los laboratorios de cómputo se instruye a los estudiantes en el uso de paquetería estadística, y para este efecto se enseñan los programas de cómputo más populares que hay entre colegas académicos y el mercado laboral, que generalmente son también los de más fácil adquisición (ej. Excel, spss, splus, sas, Eviews, etc.). Lo anterior se hace con el objetivo principal de asegurar que los estudiantes realicen sus tareas y prácticas de análisis de datos sin dificultades innecesarias. Pero ¿cómo satisfacer estos intereses académicos y objetivos pedagógicos cuando se explican conceptos y técnicas de estadística espacial dada la limitación impuesta por los altos precios de los programas de cómputo en la materia?

Este documento muestra una manera eficaz para enseñar autocorrelación espacial (ae) mediante Rookcase, un add-in gratuito del paquete Excel y disponible en internet. Precisamente, para ser más didácticos, el documento empieza con una breve descripción del significado teórico y metodológico de los datos estadísticos espacialmente autocorrelacionados.[2] Esta descripción es proseguida por un ejemplo de cómo enseñar ae de manera simple y económica.

 

2. Definición de conceptos: la autocorrelación, la dependencia y la heterogeneidad espaciales

 

Definida de manera simple, la autocorrelación espacial (ae) es la concentración o dispersión de los valores de una variable en un mapa. Dicho de otra manera, la ae refleja el grado en que objetos o actividades en una unidad geográfica son similares a otros objetos o actividades en unidades geográficas próximas (Goodchild, 1987). Este tipo de autocorrelación prueba la primera ley geográfica de Tobler (1970) que afirma: todo está relacionado con todo lo demás, pero las cosas cercanas están más relacionadas que las distantes.

La dependencia espacial (de) se produce cuando “el valor de la variable dependiente en una unidad espacial es parcialmente función del valor de la misma variable en unidades vecinas” (Flint, Harrower y Edsall, 2000: 4). Es decir, cuando la autocorrelación es sustantiva y no existe un factor de aleatoriedad. En el análisis de datos agregados geográficamente es frecuente encontrar que los valores de las variables estén autocorrelacionados espacialmente o sean espacialmente dependientes. La diferencia entre ae y de está, fundamentalmente, en el uso de las palabras y estriba en que el primer caso se refiere simultáneamente a un fenómeno y técnica estadística, y el segundo, a una explicación teórica (Vilalta, 2004).

Además de la autocorrelación y dependencia espaciales, hay otro concepto estadístico igualmente importante, la heterogeneidad espacial (he). Se refiere a la variación de las relaciones entre las variables en el espacio (LeSage, 1999). En términos teóricos, la heterogeneidad espacial se debe a una variación real y sustantiva que evidencia la existencia y la validez del contexto geográfico en la definición de un comportamiento social (O’Loughlin y Anselin, 1992). Por ejemplo: la población de cierta clase social apoya a un partido político en una ciudad o región; en otra, la población de la misma o similar clase social apoya a un partido opuesto.

La he puede presentarse debido a 1) simplemente un problema estadístico como consecuencia de la heteroscedasticidad en un modelo de regresión, o bien, 2) al igual que la de, por la existencia de una variación espacial sustantiva de la variable en cuestión; en este caso también estará presente el problema de la heteroscedasticidad.

La heteroscedasticidad se refiere a la inconstancia en los residuales de un análisis de regresión. Aquí es donde la de y la he tienen implicaciones tanto metodológicas y teóricas importantes. Si no se toma en cuenta la de en el análisis de regresión, la implicación metodológica es que los coeficientes serán ineficientes para mostrar la magnitud de la relación entre las variables. Otra consecuencia por no considerar la he será que, además de tener coeficientes ineficientes, las pruebas de significación estadística sobre ellos serán cuestionables debido a la inflación en los errores estándar (Anselin, 1988). La implicación teórico-social de la de y la he ocurre en el contexto geográfico, pues tiene un efecto parcial en el comportamiento humano (O’Loughlin y Anselin, 1992).[3]

 

3. La detección y medición de la autocorrelación espacial

 

La técnica más antigua y típica para la detección y medición de la ae es el coeficiente I de Moran (1950). Esta técnica ha sido utilizada en la investigación en México sobre desarrollo económico regional (Vilalta, 2003 y Martínez, 2004) y comportamiento electoral (Vilalta, 2004).

El diseño es similar al coeficiente de correlación de Pearson. Sus valores varían entre +1 y –1, donde el primer valor significa una autocorrelación positiva perfecta (perfecta concentración), y el segundo una autocorrelación negativa perfecta (perfecta dispersión);[4] el cero significa un patrón espacial totalmente aleatorio. La diferencia entre los dos coeficientes de Moran y Pearson se basa en que en el primer caso la asociación de valores en el conjunto de datos está determinada por una matriz de distancias o contigüidad que predefine los valores vecinos (los valores para el cómputo del coeficiente).

La formula del coeficiente I de Moran es:[5]

 

 

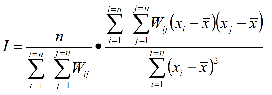
En esta fórmula, n significa el número de las unidades (es decir, áreas o puntos) en el mapa, Wij es la matriz de distancias que define si las áreas o puntos geográficos, i y j, son o no vecinos. Este coeficiente I se sujeta a una prueba de significancia estadística de valores Z, es decir, con el supuesto de una distribución normal (Cliff y Ord, 1981; Goodchild, 1987).

La dificultad de enseñar esta técnica no es conceptual sino más bien práctica; consiste en que el cómputo manual es sumamente laborioso, por lo que es necesario contar con un paquete sig que permita realizarlo; pero, como se mencionaba anteriormente, estos paquetes tienen un precio elevado.

 

4. Un ejemplo sobre cómo enseñar ae: una geografía del desempeño escolar

 

En la revisión de literatura que se llevó a cabo para la elaboración de este documento, no se encontró un solo estudio que mostrara ejemplos de tipo didáctico para la enseñanza de esta técnica. Los textos relacionados son fundamentalmente matemáticos, demostrativos y poco atractivos para el alumno universitario típico.

Para resolver esta situación, a continuación se presenta un ejemplo verídico y simple proveniente de una distribución geográfica de calificaciones parciales (o de medio término) en un salón de clases de la materia de Métodos Cuantitativos de Investigación (véase gráfica i). La clase se conformaba por 25 alumnos. El salón de clases contaba con 32 asientos; cada cuadro representa un asiento. Cabe mencionar que los estudiantes se sentaron siempre en el mismo lugar para tomar clases y presentar exámenes.

 

Gráfica i

Distribución espacial de calificaciones parciales en un salón de clases de la materia de Métodos Cuantitativos de Investigación

 

Al observar este patrón espacial de calificaciones, el profesor de estadística espacial puede tener las siguientes preguntas:

 

a. ¿Representa un patrón espacialmente aleatorio en una distribución de calificaciones?

b. ¿Los estudiantes con las mejores calificaciones se encuentran concentrados o dispersos en el salón de clases?

 

Evidentemente, este tipo de preguntas debe contestarse de manera probabilística; así, la pregunta se reformula de la manera siguiente:

 

c. ¿Cuál es la probabilidad de que este patrón geográfico no sea aleatorio?[6]

 

La forma de responderla es, precisamente, calculando el nivel de concentración o dispersión y probando si es estadísticamente aleatorio o no. Para el cálculo del coeficiente I, se utilizó en este caso la extensión Rookcase para el paquete Excel de Microsoft. Esta extensión o add-in ha sido desarrollada por Mike Sawada de la Universidad de Ottawa.[7] El programa calcula el coeficiente considerando diferentes patrones de contigüidad espacial (Sawada, 1999). En este caso se utilizó el patrón “reina” (queen), ya que en la medición desea considerarse el contacto de todos y cada uno de los vecinos (un máximo de ocho vecinos; véase la gráfica i).[8]

En el análisis espacial, la hipótesis nula significa ausencia de un patrón espacial. Esta hipótesis se prueba ubicando el coeficiente de Moran (1950) dentro de una curva normal de probabilidades. Es decir, la pregunta es si el arreglo espacial de los valores es aleatorio entre un número n de posibles arreglos.

El cuadro 1 muestra los resultados de la prueba de autocorrelación espacial a través del coeficiente I. Estos resultados indican la presencia de una autocorrelación positiva y estadísticamente significativa (I = .204, Z = 2.600); es decir, una tendencia a la concentración espacial de calificaciones. El valor de Z es mayor a 2.58, por lo que puede concluirse con un nivel de confianza de 99% que la concentración no es aleatoria, con el supuesto de una distribución normal de valores probables de Z.[9]

 

Cuadro 1

Resultados del análisis de autocorrelación espacial

 

# Obs	Mean	SD	# Neighbours
32	80.063	27.624	94

 

 

 

Lo anterior permite sugerir que la selección de asientos por parte de los estudiantes –al menos en este caso– siguió un proceso selectivo en cuanto al rendimiento de los compañeros o vecinos de banca; los estudiantes con altas calificaciones tendieron a sentarse cerca de otros con calificaciones similares, y viceversa, en el caso de aquellos con calificaciones bajas.

Aquí quedaría pendiente una prueba de de o explicativa. Por ahora sólo se ha calculado el nivel de ae. Pero seguiría buscar las causas de esta concentración, para lo que se requeriría analizar la covariación entre distintas variables junto con la variación espacial de la variable dependiente, en este caso las calificaciones, y que podría ser realizada simultáneamente a través del análisis de regresión espacial autorregresivo (Anselin, 1988 y Vilalta, 2004).

 

Conclusiones

 

Hay pocos profesores de estadística en universidades mexicanas interesados en enseñar las implicaciones teóricas y metodológicas de la autocorrelación espacial.¹⁰ Pero quienes efectivamente se interesan tienen serias dificultades para hacerlo de una forma didáctica y eficaz.

Durante la labor docente, los ejemplos de clase son siempre mudables; los cambios son a veces planeados, en otras ocasiones improvisados. Sin embargo, los ejemplos siempre se harán en relación con las experiencias de los estudiantes para lograr un efecto explicativo o aclaratorio. La experiencia muestra que cuanto más identificados estén los estudiantes con los ejercicios y ejemplos utilizados en clase, mayor será el aprovechamiento y más rápido se dará con la solución acertada. En este sentido, el mismo salón de clase puede ser utilizado como contexto para explicar la espacialidad de los procesos sociales. Los estudiantes piensan y sienten a partir de nuestras conversaciones, argumentaciones, analogías y ejemplos utilizados en clase. El autor de este documento pudo constatar que no fue sino hasta que se utilizó este ejercicio en una clase, que la perspectiva espacial de las cosas permaneció transparente y reconocible para la mayoría de los estudiantes.

De forma resumida, este documento presentó un ejercicio simple y efectivo que permite solucionar algunas de las complicaciones inherentes en la enseñanza de la autocorrelación espacial. Claramente hay otros problemas asociados al análisis de datos espacialmente autocorrelacionados; pero esos problemas no son parte de los objetivos de este trabajo.

Relacionado con lo anterior, cabe agregar que a lo largo de este documento no se comentaron otras opciones de software de estadística espacial.¹¹ La razón es que la mayoría del software en el mercado es de precio muy elevado; la ventaja del presentado en este trabajo es que es gratuito. Si en el futuro próximo los precios del software se abaratan, lo que es muy probable, el trabajo docente se vería beneficiado enormemente, a la par que los alumnos podrían adquirir conocimientos de técnicas más avanzadas en estadística inferencial para la geografía. La reducción de los precios tendría un efecto positivo en el proceso de enseñanza-aprendizaje. Mientras tanto, es necesario buscar soluciones prácticas a problemas reales, vigentes, al mismo tiempo que atraemos a los estudiantes a pensar geográficamente.

 

Bibliografía

 

Anselin, Luc (1988), Spatial Econometrics: Methods and Models, Kluwer Academic, Dordrecht.

 

Cliff, Andrew y Keilh Ord (1981), Spatial Processes: Models and Applications, Pion Limited, Londres.

 

Flint, Colin, Mark Harrower y Robert Edsall (2000), “But How Does Place Matter? Using Bayesian Networks to Explore a Structural Definition of Place”, documento presentado en The New Methodologies for the Social Sciences Conference, University of Colorado, Boulder.

 

Goodchild, Michael (1987), “Spatial Analytical Perspective on Geographical Information Systems”, International Journal of Geographical Information Systems, 1: 327-334.

 

LeSage, James (1999), Spatial Econometrics Using matlab, www.econ.utoledo.edu, agosto 2001.

 

Martínez, Juan Manuel (2004), Convergencia y divergencia regional en México: 1940-2000, tesis doctoral en elaboración, Instituto Ortega y Gasset, Universidad Complutense de Madrid.

 

Moran, Patrick, (1950), “Notes on Continuous Stochastic Phenomena”, Biometrika, 37 (1-2): 17-23.

 

O’Loughlin, John y Luc Anselin (1992), “Geography of International Conflict and Cooperation: Theory and Methods”, en Michael Don Ward (ed.), The New Geopolitics, Gordon and Breach, Filadelfia, pp. 11-38.

 

Sawada, Michael (1999), “Rookcase: An Excel 97/2000 Visual Basic (VB) Add-in for Exploring Global and Local Spatial Autocorrelation”, Bulletin of the Ecological Society of America, 80 (4): 231-234.

 

Tobler, Waldo (1970), “A Computer Movie Simulation Urban Growth in the Detroit Region” Economic Geography, 46 (2): 234-240.

 

Vilalta, Carlos Javier (2003), “Una aplicación del análisis espacial al estudio de las diferencias regionales del ingreso en México”, Economía, Sociedad y Territorio, El Colegio Mexiquense, a.c. 4 (14): 317-340.

 

_____ (2004) “Sobre la espacialidad de los procesos electorales y una comparación entre las técnicas de regresión ols y sam”, Working paper, egap-Tecnológico de Monterrey, campus Ciudad de México, disponible en: Michel Sawada, Universidad de Ottawa: http://www.uottawa.ca/academic/arts/geographie/lpcweb/newlook/members/old_members/sawada.htm y http://www.uottawa.ca/academic/arts/geographie/lpcweb/newlook/publs_and_posters/reports/moransi/moran.htm.

 

Manchester Metropolitan University, Dept. of Biological Sciences, http://149.170.199.144/.

 

 

Enviado: 10 de agosto de 2004.

Reenviado: 7 de diciembre de 2004.

Aceptado: 1 de febrero de 2004.

 

Carlos Javier Vilalta y Perdomo es doctor en estudios urbanos por la Portland State University. Se encuentra adscrito a la División de Humanidades y Ciencias Sociales del Instituto Tecnológico y de Estudios Superiores de Monterrey, campus Ciudad de México. Sus líneas de investigación tienen que ver con la geografía electoral, el desarrollo regional y la metodología política. Son sus publicaciones: “The Local Context and the Spatial Diffusion of Multiparty Competition in Urban Mexico, 1994-2000”, Political Geography, 23 (4), 2004, pp. 403-423; “The Spaces of Postmodernity: Readings in Human Geography”, Political Geography, 23 (1), 2004, pp. 104-105; “Perspectivas geográficas en la sociología urbana: la difusión espacial de las preferencias electorales y la importancia del contexto local”, Estudios Demográficos y Urbanos, 18 (3), El Colegio de México, 2003, pp. 147-177, y “Una aplicación del análisis espacial al estudio de las diferencias regionales del ingreso en México”, Economía, Sociedad y Territorio, 4 (14), El Colegio Mexiquense, 2003, pp. 317-340.