Evolución del Producto
Interno Bruto en México, 1921-1995:
¿Declinación o Histéresis?
Evidencia adicional*
Pablo Mejía Reyes/Zeus S.
Hernández Veleros
El Colegio
Mexiquense/Instituto Nacional de
Migración
Resumen
Se analiza el comportamiento
de largo plazo del PIB per cápita real de México (1921-1995) con el fin de
determinar si tiene una tendencia estocástica −raíz unitaria y los choques
corrientes tienen un carácter permanente o una determinista− o bien no tiene
raíces unitarias y los choques son transitorios. Se hace especial énfasis en el
análisis de los efectos de la desaceleración de la producción a partir de la
década de los ochenta. Para hacerlo, empleamos diferentes técnicas de series de
tiempo. Aunque los resultados no son contundentes, con base en las propiedades
de las pruebas empleadas, nos inclinamos a pensar que la tendencia es
determinista y, por tanto, los choques son transitorios, aunque se encuentra
evidencia de una elevada persistencia que hace muy lenta la reversión a la
tendencia de largo plazo. En ese sentido, los resultados de este documento
impugnan la hipótesis de la inefectividad de la política económica.
*Una versión preliminar de este documento fue presentada en el VI
Coloquio Nacional de Economía Matemática y Econometría, Universidad de las
Américas, Puebla, Pue. La asistencia de investigación de Alfredo Ríos Sara fue
muy importante.
En los años recientes ha
resurgido el interés por el estudio de temas asociados al crecimiento económico
de largo plazo. Parte del debate se ubica en la explicación de la naturaleza y
fuentes de las fluctuaciones de la producción. Una vertiente muy importante en
la literatura analiza este aspecto sobre todo desde una perspectiva estadística
caracterizando el comportamiento de largo plazo del producto, para lo cual ha
desarrollado diferentes metodologías que tratan de determinar si el producto de
una nación sigue una tendencia determinista o una tendencia estocástica, o bien
si no puede o es posible caracterizarse como un proceso que sigue un camino
aleatorio, respectivamente. Las implicaciones en cada caso son muy diferentes:
el primero conlleva un carácter predecible de la serie y transitoriedad de los
efectos de los choques sufridos por esa variable, en tanto que el último
permite obtener conclusiones completamente contrarias. Son muchos los trabajos
que se han realizado, principalmente en los Estados Unidos, pero aún existe un
amplio debate respecto a las implicaciones políticas de la existencia de un
tipo u otro de tendencia.
El largo periodo durante el
cual la economía mexicana ha tenido bajas o nulas tasas de crecimiento
económico obliga a reflexionar sobre la naturaleza de los efectos desfavorables
que la economía ha experimentado, así como a indagar sobre sus perspectivas del
crecimiento.
De hecho, la experiencia de
México ha sido muy accidentada a lo largo de su historia. Durante el periodo
que se analiza (1921-1995) se presentaron periodos de elevado y sostenido
crecimiento, pero también grandes recesiones. La historia económica moderna se
puede dividir en varios subperiodos de acuerdo con el tipo de políticas
instrumentadas y con la dinámica económica general, destacando tres de singular
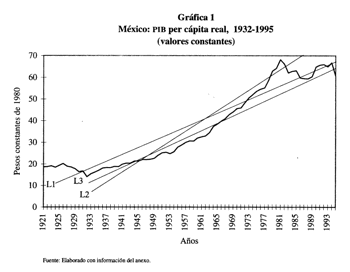
importancia, tal como se aprecia en la gráfica 1: el periodo en torno a la gran
recesión del capitalismo mundial, caracterizado por un decrecimiento mayúsculo
del producto per cápita real, cuyos efectos se han diluido en el tiempo;
seguido de otro de rápida recuperación, como lo muestra el crecimiento
sostenido entre 1932 y 1981; finalmente, el de la década de los ochenta hasta
el periodo actual, cuando el crecimiento se ha desacelerado según parece de
manera permanente.
Por lo reciente y la
actualidad de sus efectos, es de particular importancia destacar el efecto de
las crisis −por lo visto recurrentes− que han caracterizado a la economía
mexicana durante las dos últimas décadas. La primera se presentó en 1976 y pudo
superarse sólo por el descubrimiento de importantes yacimientos de petróleo. La
vulnerabilidad del crecimiento económico basado en la explotación de este
recurso se manifestó con la caída del precio del crudo en el mercado mundial a
principios de los ochenta y el elevado endeudamiento externo a plazos conos y a
tasas de interés elevadas (Ros, 1987). En consecuencia, la crisis económica
reapareció a partir de 1982. Luego de varios años de intentos fallidos de
estabilización,[1]
la economía pudo repuntar a partir de 1988, pero desde diciembre de 1994 se
encuentra sumida en un nuevo episodio de recesión. Lo relevante en este sentido
es conocer los efectos de la desaceleración en el crecimiento de la producción.
Información preliminar al
respecto es presentada en la gráfica 1: excluyendo los periodos inicial y final
de decrecimiento o desaceleración de la producción, se puede observar un
crecimiento sostenido entre 1932 y 1981; cuando se incluye el primero o el
último periodo de tiempo, la tasa media anual de crecimiento disminuye en 0.4 y
0.2%, respectivamente, en tanto que cuando se incorporan ambos periodos, la
misma tasa disminuye en 0.9%. Los efectos de estas variaciones se tratan de
captar mediante las rectas tendenciales dibujadas en la misma gráfica 1: L1
representa una hipotética tendencia lineal para el periodo completo y es la
menos inclinada de las tres, indicando la menor tasa media anual. L2 se refiere
al periodo de crecimiento sostenido durante las etapas de crecimiento mediante
la sustitución de importaciones y de desarrollo estabilizador, y culmina con el
auge petrolero; es la más inclinada e indica una tasa de crecimiento media
mayor. Finalmente, L3 es la que incorpora a la anterior la desaceleración
económica iniciada a principios de la década pasada; es más acostada que L2,
mostrando los efectos de la crisis sobre el crecimiento medio anual. En estas
condiciones es muy importante usar técnicas más poderosas para conocer las
implicaciones de largo plazo del comportamiento del producto durante el último
subperiodo.
Así pues, el objetivo del
presente documento es analizar el comportamiento del producto interno bruto per
cápita real de México con el fin de determinar la naturaleza de los estragos (o
de la tendencia subyacente) que la economía mexicana ha experimentado a lo
largo de este siglo, destacando la desaceleración en su crecimiento a partir de
la década anterior. Para ello, se utilizan técnicas de descomposición de series
de tiempo en sus componentes permanente y transitorio; pruebas de raíces
unitarias que permiten determinar el tipo de tendencia subyacente y, por tanto,
la naturaleza de los obstáculos que enfrenta la variable en cuestión; y medidas
de persistencia que indican también el tipo de tendencia, y como se deduce de
su nombre, el tiempo requerido para retornar a la senda de largo plazo.
Este documento está dividido
en las siguientes partes. En la primera se hace una revisión de la literatura
existente sobre el tema, destacando el debate teórico en torno a las
implicaciones de política y a la naturaleza estadística de un trabajo de este
tipo. Después se abordan algunas consideraciones relacionadas con las pruebas
de series de tiempo que han de emplearse. Finalmente, estas últimas se aplican
para llegar a algunas conclusiones.
I. Debate teórico-empírico
El amplio debate en la
literatura sobre la naturaleza y las fuentes de las fluctuaciones económicas y,
particularmente, respecto a la trascendencia de las implicaciones de la
existencia de una tendencia estocástica (raíz unitaria) o una determinista (raíz
menor a la unidad), ha tenido lugar tanto en lo teórico como en lo empírico. En
el primer caso, existen diferentes posiciones analíticas en discusión. Por un
lado, la posición keynesiana tradicional considera que las fluctuaciones son
sobre todo transitorias, y supone que surgen de eventos provenientes del lado
de la demanda (tales como cambios en la política fiscal, en los gustos, en los
espíritus animales, etcétera). Considera que las series macroeconómicas tienen
un componente cíclico aleatorio que fluctúa en torno a un componente tendencial
determinista, asociado al crecimiento secular de la serie.
Por su parte, los
monetaristas consideran que las fluctuaciones en la demanda agregada,
provocadas por la política monetaria, podrían tener efectos de corto plazo
sobre la producción y el empleo, pero que a la larga la economía necesariamente
regresará a su tasa natural (Frisch, 1986).
Para la nueva escuela clásica
de los ciclos económicos reales, las fluctuaciones se deben en gran medida a
los choques permanentes del lado de la oferta. Toma los choques en la
productividad como la fuente de los ciclos económicos: si las fluctuaciones en
el producto son básicamente permanentes, entonces los choques en la oferta,
como los tecnológicos o los del mercado de trabajo, son importantes para
explicar las fluctuaciones que ocurren. Interpretan la existencia de una raíz
unitaria en el proceso generador del PLB per cápita real como un argumento a su
favor (Mankiw, 1992).
Sin embargo, los llamados
nuevos keynesianos han cuestionado esta posición haciendo hincapié en la
competencia imperfecta, los mercados incompletos, la incertidumbre, la
posibilidad de equilibrios múltiples y de fallas de coordinación, como
condiciones que pueden inducir persistencia en la serie del producto, dando
lugar a la permanencia de los choques que provienen de la demanda y, por tanto,
la existencia de una raíz unitaria. Específicamente, Blanchard y Kiyotaki
(1987) construyen un modelo de competencia monopólica con elementos externos
provenientes de la demanda agregada que, junto con pequeños costos de menú,
implican la posibilidad de que la demanda afecte la producción y el bienestar,
particularmente por cambios en la cantidad nominal de dinero. A su vez,
Blanchard y Summers (1988) hablan de los efectos histéresis referentes a
que cuando la economía ha estado lejos de su tasa natural de desempleo puede
retardarse el retorno a razón del tiempo que esté alejada de ella, situación
por la que la economía estaría permanentemente en posiciones de equilibrio
frágil y altamente sensibles a los efectos corrientes y dependientes de la
historia. Por su parte, Durlauf (1991) destaca los mercados incompletos y las
fallas de coordinación como condiciones en las que los choques tecnológicos
pueden tener efectos persistentes. Finalmente, sobre una base más empírica,
Nelson y Plosser (1982) junto con Campbell y Mankiw (1987a) consideran que si
la aproximación de raíz unitaria es una buena aproximación para el producto,
entonces es poco probable que los impactos nominales del lado de la demanda
puedan provocar las fluctuaciones económicas; en cambio, serían los factores
reales los que explicarían mejor los cambios observados en la producción debido
a su mayor importancia en la determinación del componente secular o permanente.
Sin embargo, West (1988) presenta un modelo consistente con la hipótesis de la
tasa natural de desempleo en el que los ajustes monetarios, sin ser los únicos
o más importantes determinantes, pueden generar suficiente persistencia en el
producto para que aparezca una raíz casi unitaria.
Los resultados de la
investigación empírica, por otro lado, permiten la obtención de conclusiones
contradictorias. En un trabajo pionero donde se impugnó por vez primera el
carácter determinista del crecimiento secular de las variables, Nelson y
Plosser (1982), analizan las funciones de autocorrelación de varias series, en
nivel y en primeras diferencias, de los Estados Unidos, y aplican la prueba de
Dickey-Fuller aumentada (DFA); en la mayoría de los casos (incluido el producto
nacional bruto per cápita real) no pueden rechazar la hipótesis de existencia
de una raíz unitaria o de una tendencia estocástica (proceso estacionario en
diferencias), aunque reconocen que sus pruebas carecen de poder ante la
hipótesis alternativa de un proceso estacionario en tendencia con una raíz
autorregresiva cercana a 1. Al respecto, Campbell y Mankiw (1987a) utilizan
medidas de persistencia y funciones de autocorrelación para caracterizar las
fluctuaciones económicas, y encuentran que éstas son más persistentes de lo
esperado. Campbell y Mankiw (1987b) construyen modelos ARIMA para la serie
trimestral del producto de los Estados Unidos, y mediante funciones de
impulso-respuesta determinan que los choques tienen un carácter permanente, en
tanto que la medida de persistencia de Cochrane les permite encontrar una
elevada persistencia. Cochrane (1988) critica las pruebas convencionales de
raíces unitarias argumentando que tienen escaso poder porque no pueden
distinguir entre el componente camino aleatorio y el componente estacionario
propios de toda serie temporal, por lo que propone una medida de persistencia
basada en la razón de las varianzas del componente aleatorio y de los valores
observados de la serie; así, encuentra que el producto nacional bruto regresa a
su tendencia tras un choque en un horizonte temporal propio del ciclo
económico. Perron (1988) analiza las mismas variables que Nelson y Plosser y
algunas otras mediante los estadísticos propuestos por él mismo y por Phillips,
y encuentra que las series, en general, tienen una tendencia estocástica;
resultado particularmente cierto para el producto nacional bruto per cápita
real. Por su parte, Balke (1991) halla evidencia en favor de una tendencia
determinista con las pruebas de raíces unitarias de DFA y Phillips- Perron
(PP), al igual que con la razón de varianzas de Cochrane y las funciones de
impulso-respuesta obtenidas con modelos ARIMA. Redebusch (1993) aplica la
pruebas de DFA (una prueba de DF corregida), la prueba de Phillips y la prueba
de razón de verosimilitud, y en ningún caso puede rechazar la hipótesis de raíz
unitaria, lo que lo lleva a cuestionar su poder para distinguir entre un modelo
estacionario en tendencia de uno estacionario en diferencias. Durlauf (1993)
considera que Campbell y Mankiw (1987b) y Cochrane (1988) llegan a conclusiones
diferentes debido a que analizan distintos aspectos de la función de densidad
espectral del mismo modelo; él analiza la función de distribución espectral (y
la de densidad espectral de los cambios del producto, la cual está basada en
las autocorrelaciones de corto y de largo plazo), y encuentra que en periodos
cortos la representación de camino aleatorio con desplazamiento es adecuada, en
tanto que en periodos largos las fluctuaciones se caracterizan por una
sustancial persistencia. Finalmente, Moscan (1994) utiliza un modelo
estructural de series de tiempo y tampoco puede rechazar la hipótesis de
tendencia estocástica.
En el caso de México, es
curioso que un tema que ha recibido tanta atención en la literatura
internacional no haya sido analizado con tanto detalle para este país. De
hecho, existe tan solo un trabajo que trata el tema. Ruprah (1991) analiza la
estacionariedad del PIB per cápita real de México en torno a una tendencia
determinista empleando la prueba de raíces unitaria de DFA, la razón de
varianzas y la medida de persistencia de Cochrane y análisis de cointegración;
así, encuentra evidencia en favor de la hipótesis de que existe una tendencia
estocástica.
Considerando que West (1988)
argumenta que en muestras finitas es difícil distinguir entre una raíz unitaria
y una raíz arbitrariamente cercana pero menor a 1, el análisis univariante del
producto de un solo país es poco útil para distinguir entre teorías
estacionarias y no estacionarias, o entre modelos en los que los ajustes
monetarios son más importantes que aquellos que no lo son, aquí, al igual que
en Cochrane (1988), el análisis tendría fundamentalmente relevancia
estadística.
II. Temas de Econometría
1.
Tendencias deterministas y estocástica[2]
A grandes rasgos, una serie
temporal económica (yt) se forma por dos componentes que pueden ser
aleatorios: 1) cíclico (ct), que captura las fluctuaciones
temporales asociadas con el ciclo económico; y 2) tendencial (xt),
que describe el crecimiento económico de largo plazo.
Anteriormente se consideraba
que la volatilidad en las series de tiempo estaba asociada con las
fluctuaciones en el componente cíclico, y no con fluctuaciones en la tendencia.
Tras el trabajo de
Nelson y Plosser (1982) se
acepta que la tendencia de muchas series temporales fluctúa aleatoriamente en
el tiempo. Considérese el modelo que describe la serie yt
donde el componente ct
es unavariable estocástica estacionaria (media, varianza y autocovarianzas
incondicionales son constantes en el tiempo) con media cero. El componente
tendencial (xt) puede ser determinista o aleatorio. En el primer
caso tenemos una tendencia temporal lineal expresada por:
donde el cambio en la
tendencia, dado por la variación en la variable, es igual a la constante b.
Una tendencia estocástica, a su
vez, puede ser expresada por:
donde E es un ruido
blanco gaussiano, es decir, E se distribuye idéntica e independientemente de
acuerdo con una distribución normal con media cero y varianza finita e igual a
d. Sustituyendo sucesivamente xt-i en (3) obtenemos:
donde el componente aleatorio
permanente está dado por el último término y el componente determinista
permanente por los primeros dos. Si xo = 0,
es decir, los primeros
momentos no son independientes del tiempo.
De la última expresión se
observa que el componente tendencial depende no sólo de la tasa de crecimiento
promedio (a), sino también de todos los valores pasados de Et, lo
cual muestra que los cambios en el componente tendencial son permanentes. Un
caso de especial importancia por sus implicaciones es el conocido como paseo
aleatorio, cuya naturaleza de hecho ha sido explicada en el caso de la
tendencia estocástica.
La situación más general
puede verse en la ecuación (3) si la consideramos como un proceso
autorregresivo de orden 1, AR(1), con un parámetro a, es decir
donde tras sustituciones sucesivas
y a medida que t se incrementa con |a| < 1 obtenemos:
Contrariamente, cuando b
= 1 tendremos un resultado igual a la expresión (4). Es decir, la presencia de
un coeficiente autorregresivo igual a 1 es equivalente a la presencia de una
tendencia estocástica, lo que a su vez implica la existencia de una raíz
unitaria.
Como en el análisis aquí realizado
se trata de determinar la estacionariedad de la serie en torno a una tendencia
determinista, sería útil presentar un modelo análogo al anterior que incorporara
estas consideraciones. Sea el modelo siguiente:
donde Et, sigue
un proceso ruido blanco gaussiano. Dado un valor inicial x, y sustituyendo
sucesivamente obtenemos
De esta formulación se sigue
que la serie converge solamente cuando |y| < 1. Así, a medida que t
se hace muy grande, se puede mostrar que el criterio de la razón para el primer
término converge a y en tanto que para el segundo lo hace a y-1;
el cuarto término se hace también muy pequeño. Por lo tanto, la expresión
anterior se reduce a una constante correspondiente al desplazamiento (drift)
de la serie, una tendencia determinista y la suma de los cambios corrientes que
experimenta la serie y que son cada vez menos importantes en su comportamiento,
por lo que ésta sería estacionaria en torno a dicha tendencia. En caso
contrario, con |y| ≥ 1, la serie no convergería y no existiría tendencia
alguna hacia la cual retornar.
Las implicaciones de la
existencia de una raíz unitaria son particularmente importantes cuando se
analiza la naturaleza de las fluctuaciones económicas. Entre las más relevantes
cabe destacar que: los cambios tienen efectos que no se disipan; es posible que
trabajemos con correlaciones espurias si las variables en cuestión (o algunas
de ellas) son paseos aleatorios; la tendencia de la serie será no estacionaria
y estocástica. Esto tiene también implicaciones en los pronósticos, ya que
serían diferentes para una serie aleatoria o para una serie determinista, al
igual que los grados de incertidumbre asociados con ellos: los pronósticos de
largo plazo de un paseo aleatorio cambian continuamente ante los cambios
corrientes que experimenta la serie; la habilidad de los métodos econométricos
convencionales para la inferencia de los parámetros difiere; por ejemplo, los
mínimos cuadrados ordinarios no llevarían a un estimador del parámetro
consistente; y las pruebas de hipótesis que descansan sobre la teoría de la
distribución asintótica son sensibles a la presencia de una tendencia
estocástica.[3]
2. Las
pruebas empleadas
En primer lugar se analiza la
dinámica de los componentes permanente y transitorio del PIB per cápita real,
empleando la metodología propuesta por Beveridge y Nelson (1981) con el objeto
de caracterizar los efectos de los periodos de crisis en el comportamiento de largo
plazo del crecimiento de la economía mexicana. Posteriormente, se pretende
delimitar el tipo de tendencia seguida por la misma variable, para lo cual se
emplean distintas técnicas a fin de determinar la presencia de raíces
unitarias. Específicamente, utilizaremos las propuestas de Dickey y Fuller,
Phillips y Perron y Sims. Finalmente, desde una perspectiva un tanto diferente,
se empleará la medida de persistencia de Cochrane. Estas metodologías se
resumen a continuación.
A diferencia del tratamiento
tradicional que se hacía en el estudio de los ciclos económicos -en el que se
consideraba a éstos como las fluctuaciones en torno a una tendencia
determinista, es decir, en un modelo estacionario en tendencia (Nelson y
Plosser, 1982)−, el enfoque de descomposición de Beveridge y Nelson (1981)
−basado en el modelo estacionario en diferencias propuesto por Nelson y Plosser
(1982)− acepta que las fluctuaciones observadas pueden provenir también de
cambios en su tendencia de largo plazo. En ese sentido, se reconoce que el
componente de largo plazo es estocástico en virtud de que las innovaciones de
cada periodo afectan el nivel de ingreso estocástico de estado estacionario.
Este constituye el componente permanente y es obtenido mediante la construcción
de un modelo ARIMA (p, 1, q) para la serie. En cada periodo el
componente permanente es la suma del valor corriente más los valores
pronosticados desde t hasta k, obtenidos del modelo ARIMA. El
componente transitorio o cíclico es la diferencia entre el valor observado de
la serie y el componente permanente. El componente permanente se relaciona con
el crecimiento económico, determinado principalmente por factores tales como
acumulación de capital, crecimiento poblacional y cambio tecnológico, en tanto
que el componente cíclico se asume transitorio (y estacionario), relacionado
con factores monetarios, y tal vez, aunque en menor magnitud, reales. Puesto
que las fluctuaciones cíclicas se disipan en el tiempo, cualquier movimiento de
largo plazo o permanente (no estacionario) se atribuye necesariamente al
componente secular.
En el caso de las pruebas de
raíces unitarias, la prueba Dickey-Fuller aumentada (DFA) evalúa si el
coeficiente autorregresivo de la variable de interés es igual o diferente de 1
(Dickey y Fuller, 1981; Harvey, 1991). Se calcula con mínimos cuadrados
ordinarios; la prueba se realiza con base en el estadístico "t"
que resulta de la regresión, y se compara con la tabla de valores críticos
ofrecida por Fuller (1976), en virtud de que bajo la hipótesis nula, su
distribución limitante no es una normal. Con la finalidad de que las
innovaciones del modelo no presenten correlación serial, se introducen rezagos
de las diferencias de la variable.
La prueba de Phillips-Perron
(PP) (Perron, 1988) evalúa, a partir de un enfoque no paramétrico, la
existencia de una raíz unitaria con estadísticos válidos no obstante que las
innovaciones estén distribuidas heterogéneamente y/o que presenten débil
dependencia. La principal ventaja de esta aproximación es que, además de permitir
una amplia gama de mecanismos generadores de errores, los estadísticos de
prueba requieren sólo la estimación de un modelo autorregresivo de primer orden
por mínimos cuadrados ordinarios y de un factor de corrección basado en la
estructura de los residuos de la regresión propuesta por ellos. (Los valores
críticos también se toman de Fuller [1976]).
Las pruebas anteriores han
sido cuestionadas por su incapacidad para distinguir entre una raíz unitaria y
un coeficiente autorregresivo muy cercano pero menor a 1 (Sims, 1988; Cochrane,
1988).[4] Sims
(1988) plantea que las pruebas convencionales ponderan excesivamente la
hipótesis nula de existencia de una raíz unitaria, por lo que sugiere un examen
a partir del enfoque bayesiano -aun cuando no está muy de acuerdo con buscar
raíces unitarias exactas- en el cual la probabilidad previa que se asigna a la
hipótesis nula de raíz unitaria es modificada en un intento por ponderar
adecuadamente la evaluación. Sugiere emplear una probabilidad previa de 0.2
(Sims y Uhlig, 1991).
Finalmente, plantea que una
serie está conformada por un componente camino aleatorio (que refleja las
variaciones permanentes) y un componente estacionario (que indica las
variaciones transitorias), por lo que las pruebas de raíces unitarias que
tratan de distinguir entre series con un componente paseo aleatorio de otras
sin este componente tienen, necesariamente, escaso poder. Por lo tanto, una
medida de persistencia, la cual mide el tamaño del componente paseo aleatorio
de la variable en cuestión a partir de analizar la razón de la varianzas (Vk)
de la variable, con lo que se puede determinar el tipo de tendencia de la
serie. Si esta razón tiende a cero cuando k tiende a infinito, entonces
estamos en la presencia de una tendencia determinista, pero si Vk,
tiende a 1 al crecer k hasta infinito se tiene una tendencia
estocástica. Asimismo, define la variabilidad de largo plazo como un indicador
que muestra cuánto tardará la serie en regresar a su tendencia determinista de
largo plazo, si ésta existe.
III. Evidencia empírica
Las metodologías consideradas
antes se emplean en el caso mexicano. Se analiza el logaritmo del PIB per
cápita real de México durante el periodo 1921-1995 (yt), con
el objeto de conocer la naturaleza de los cambios que experimenta, o
equivalentemente, para determinar la naturaleza de la tendencia subyacente.
Merece especial énfasis el análisis de los efectos de la desaceleración de la
economía mexicana iniciada a principios de la década anterior. Tal serie es
empleada con el objeto de inducir homocedasticidad y eliminar la no
estacionariedad derivada de la inflación y del crecimiento poblacional
(Cochrane, 1988).
1.
Componentes permanente y transitorio
El modelo general sugerido
por Beveridge y Nelson (198 1) se formula en los siguientes términos:
donde y, representa el
logaritmo del PIB per cápita real, y su primera diferencia entonces se refiere
a su tasa de crecimiento anual; 
es la tasa de
crecimiento media del producto, y la serie e1, significa las
desviaciones con respecto a la media, las cuales pueden representarse por el
proceso estacionario e invertible representado en (9); es decir que las
desviaciones con respecto a la media, provenientes de las innovaciones de cada
periodo incluidas en ut,, son transitorias y persisten por un número
de periodos determinado por la estructura autorregresiva de e1,
pero afectan el nivel del ingreso hacia arriba o hacia abajo de manera
permanente; las expresiones 
(L) y 
(L)
representan los polinomios autorregresivo de orden p y de media móvil de
orden q, respectivamente, y u, sigue un proceso ruido blanco.
El modelo propuesto asume que
la tasa media de crecimiento se mantiene inalterada a lo largo del periodo, lo
cual es rechazado por los hechos estilizados.[5] Para
superar esta restricción, retomamos la metodología propuesta por Cuddington y Urzúa
(1988) para permitir cambios en la tasa de cfecimiento media para subperiodos
en los que se detecten cambios estructurales bien definidos. En este punto
siguen la metodología de análisis de intervención sugerida por Box y Tiao
(1975).
El modelo estimado y los
resultados para la serie que nos ocupa fueron los siguientes[6]:
donde F1 = 1 durante
el periodo 1921-1932, y 0 para el resto del periodo; F2 = 1 en 1932, y 0
los demás años; F3 = 1 durante 1982-1995, y O el periodo anterior; y F4
= 1 en 1995, y O durante los demás años; Q es el estadístico de
Ljung-Box con 18 grados de libertad; s es la desviación estándar de la
regresión; los números entre paréntesis son los estadísticos t
correspondientes. Se identificó este modelo una vez realizado el análisis de
intervención de acuerdo con las observaciones mencionadas en la nota 7. La
información reportada en (12) permite concluir que se trata de una
representación adecuada: los coeficientes son estadísticamente significativos,
el estadístico Q permite rechazar la hipótesis de correlación serial, y
las funciones de autocorrelación y de autocorrelación parcial no permiten
identificar un modelo plausible para los residuos.[7]
Para obtener el componente
permanente se siguió la metodología propuesta por Cuddington y Winters (1987)
basada en la función de ganancia de estado estacionario que obliga a usar la de
Beveridge y Nelson (1981) solamente para un periodo −en este caso, para el
último periodo, tal como lo hacen Cuddington y Urzúa (1989)− y permite obtener
directamente los efectos de las innovaciones corrientes sobre el cambio
permanente de la serie.
Se pronosticó a partir de
1995 en un horizonte de 100 periodos y se utilizó la función de ganancia
siguiente, obtenida haciendo L = 1 en (12):
Esta formulación de la
función de ganancia, donde en el lado izquierdo aparecen ahora las variaciones
en el componente permanente de y, denotado por ypt,
incorpora los cambios en la media (cambios estructurales) en el componente
permanente (tal como hacen Cuddington y Urzúa, 1988:185-186), y en ese sentido
permite la existencia de diferencias en la media permanente para los distintos
episodios en que se ha dividido el periodo total. También sugiere que 62% de
cada choque corriente tiene efectos permanentes sobre el nivel de la serie yt
; una variación de ut, unidades, que desplaza la
tendencia de largo plazo en 0.62 ut, empuja yt
en (1 - 0.62)ut unidades por encima de su tendencia durante
los periodos t, t + 1, t + 2 y t + 3, pero en t
+ 4 se reduce 38%, y de esa forma regresa a su senda de crecimiento de largo
lazo previamente ajustada por la innovación (Cuddington y Urzúa, 1988:188).
El componente permanente de
1995 se obtiene como la suma del valor del PIB per cápita real corriente y los
valores pronosticados hasta 100 periodos hacia adelante. Obtenido este valor se
resolvió (13) hacia atrás, como sugieren Cuddington y Urzúa (1989). Los
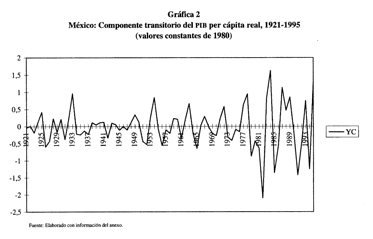
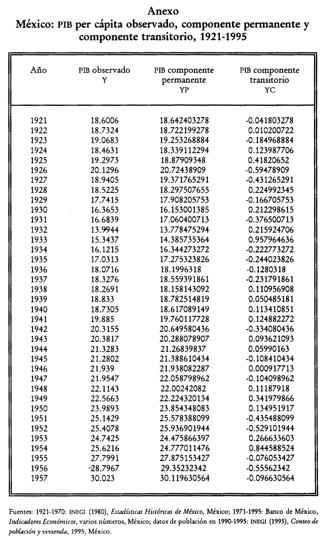
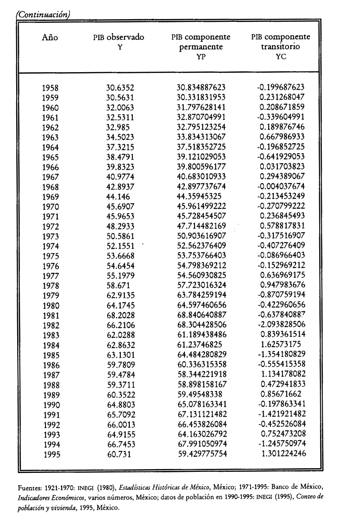
resultados aparecen resumidos en las gráficas 2,3 y 4 y en el cuadro 1; los
valores completos se encuentran en el anexo; Y representa el valor del PIB per
cápita real observado, YP es su componente permanente, y YC el componente
transitorio.
La comparación de las medias
de Y y YP muestra un comportamiento medio muy parecido entre los valores
observados y el componente permanente del PIB per cápita real, reflejando la
elevada importancia del último. Evidentemente la incorporación de los periodos
de crisis reduce la media del crecimiento, pero de especial importancia es lo
acontecido con los periodos 1932-1981 y 1932-1995, ya que después de que en el
primero de éstos creció en mayor medida el componente permanente, durante el
segundo se perdió ese efecto y los valores observados crecieron en mayor
medida. Asimismo, resulta de gran importancia destacar que la caída de más de
9% en el valor observado del PIB per cápita real durante 1995 tiene un carácter
fundamentalmente permanente.
En la gráfica 2, por otra
parte, se presenta el componente transitorio; es muy claro el incremento en su
varianza a partir del periodo conocido como el auge petrolero, justo cuando el
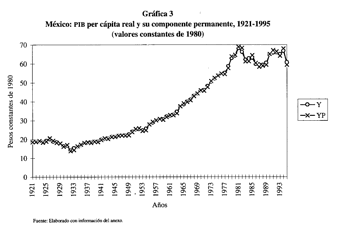
crecimiento sostenido se interrumpe. En la gráfica 3 se observa un
comportamiento muy similar entre los valores observados de la serie y su
componente permanente, reflejando la elevada proporción que éste representa en
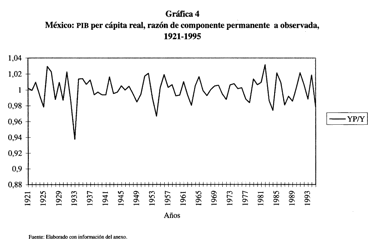
los valores corrientes. Finalmente, la gráfica 4 muestra la razón YP/Y, en la
que se aprecia que en la mayor parte de los últimos quince años el componente
permanente del PIB per cápita real ha estado por debajo de su valor observado,
indicando un deterioro más profundo del que podría inferirse del análisis de
los valores observados.
2.
Raíces unitarias
Se realizaron las pruebas
para diferentes periodos, dependiendo de si se incorporaban o no los episodios
de crisis, tanto el de la década de los años veinte como el iniciado la década
anterior. El objetivo es hacer explícitos los efectos de tales episodios.
Las pruebas se realizaron
incorporando una tendencia determinista para analizar si las fluctuaciones del
PB per cápita son estacionarias en torno a esa tendencia, es decir, para
determinar si se mueven alrededor de un valor determinista cambiante en el
tiempo, pero hacia el cual convergen en el largo plazo. Los resultados de las
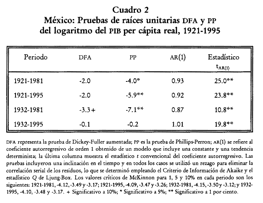
pruebas de DFA y PP aparecen en el cuadro 2.
La penúltima columna muestra
el coeficiente autorregresivo obtenido en un modelo de orden 1 que incluye
tendencia e intercepto. En los primeros dos periodos, en los que se incluye la
crisis al inicio de los años treinta y la reciente, se obtuvo un coeficiente
elevado, pero menor a 1. En el periodo de crecimiento estable y sostenido
(1932-1981), ese coeficiente fue menor a 0.9. Finalmente, en el último periodo,
cuando se excluye la gran depresión y se incluye la declinación iniciada en la
década de los ochenta, se obtuvo un coeficiente mayor a 1. A partir de esta
información podríamos esperar que en el tercer periodo la serie fuera
fundamentalmente estacionaria, y que en el último ocurriera lo contrario.
De acuerdo al criterio de
Dickey-Fuller, la inclusión de los episodios de crisis al principio y/o al
final del periodo completo provoca que la hipótesis nula de existencia de una
raíz unitaria no pueda ser rechazada. El subperiodo 1932-1981, de crecimiento
sostenido, es el único en el que, aunque débilmente, se puede rechazar tal
hipótesis. Por lo tanto, podemos concluir que en general la serie estudiada
tiene una tendencia estocástica. Sin embargo, vale la pena resaltar que una vez
que la economía asimiló la declinación al principio de la década de los
treinta, hubo un crecimiento sostenido que permitió definir una tendencia
determinista en torno a la cual fluctuaba hasta principios de la década
anterior. Este resultado cambia radicalmente cuando se incorpora al análisis la
declinación iniciada en esa misma década.
Con la prueba propuesta por
Phillips y Perron se evaluó la misma hipótesis y los resultados aparecen
también en la cuadro 2. Aunque solamente se reporta lo obtenido para I = 1, las
pruebas se hicieron para distintos valores del parámetro de truncación I; se
observó que los resultados eran insensibles a cambios en tal parámetro.[8] En los
tres primeros periodos considerados no puede aceptarse la hipótesis nula de
raíz unitaria, por lo que se concluiría que la serie presenta una tendencia
determinista en esos casos. Solamente en el último periodo, cuando se incorpora
la desaceleración en el crecimiento de la economía mexicana, se tiene como
resultado que la tendencia del PIB per cápita es estocástica. Dado que la
prueba PP es válida en un contexto más amplio que la DFA, durante esta etapa la
evidencia sugiere la existencia de una tendencia determinista hasta principios
de los años ochenta.
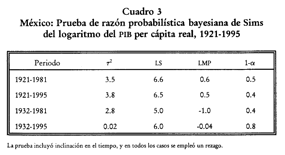
Finalmente, en el cuadro 3 se
ofrecen los resultados de la prueba de Sims. La segunda columna es el
estadístico T2, que debe ser comparado con el valor reportado
en la cuarta columna, que es el límite para muestras pequeñas (LMP): si T2
> LMP la hipótesis nula (no estacionaridad o existencia de una raíz
unitaria) no es aceptada.[9] En la
última columna se presenta la medida (1 - 
* ), que nos indica la probabilidad previa que
debería asignarse a la hipótesis nula para forzar al criterio de Sims a
aceptarla (originalmente esta probabilidad es 0.2). Cuando evaluamos la
hipótesis nula de raíz unitaria incluyendo tendencia, la hipótesis nula es
rechazada en todos los casos, pues tendríamos que asignarle una probabilidad
previa de por lo menos el doble para aceptarla, lo cual es consistente con la
relación entre T2 y el LMP.[10] En
resumen, la prueba de Sims reporta estacionaridad de la variable si se toma en
cuenta la presencia de una tendencia; es decir, la serie tendría una tendencia
determinista hacia la cual retornar en el largo plazo.
3. Razón
de varianza de Cochrane
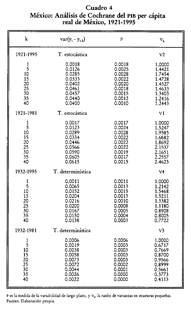
En este caso, como en los
anteriores, se subdividió el periodo completo en los siguientes subperiodos:
1921-1981, 1921-1995, 1932-1981 y 1932-1995: los resultados aparecen en el
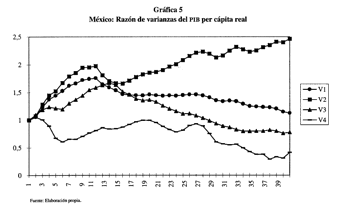
cuadro 4 y en la gráfica 5. Para determinar el tipo de tendencia de la variable
se debe observar el valor de convergencia de la razón de varianzas, Vk:
en los primeros dos casos, denotados como V1 y V2, cuando se incluye la
declinación de principios del periodo asociada con la recesión del capitalismo
mundial, su valor no regresa a cero sino que es mayor que 1 para un valor de k
= 40; esto sugiere la presencia de una tendencia estocástica o un tamaño muy
grande de su componente camino aleatorio, por lo que los choques a la variable
serían principalmente permanentes. La exclusión de tal subperiodo inicial
provoca que el valor de la razón de varianzas (V3 y V4) tienda a cero, lo cual
sugiere la presencia de una tendencia determinista y un carácter esencialmente
transitorio de los choques corrientes debido a la menor importancia del
componente camino aleatorio.
El análisis de la medida de
variabilidad de largo plazo (P) sugiere que en el periodo 1932-1981 se
requerirían 19 años para retornar a la tendencia de largo plazo, denotada por
L2 en la gráfica 1, en tanto que para el lapso comprendido entre 1933 y 1995
serían necesarios 13 años. En principio, este resultado parece insostenible
dado que el segundo de estos periodos considera los nocivos efectos de la
recesión actual de la economía mexicana. Una explicación posible podría ser que
la tendencia considerada en el segundo lapso difiere de la del primero. En la
gráfica 1 la nueva tendencia se representa por L3 y aparece más aplanada,
indicando una tasa de crecimiento medio menor. En realidad, según se observa en
el cuadro 1, la tasa de crecimiento media entre 1932 y 1981 fue de 2.54%, y la
del periodo 1932-1995, de 2.36. Considerando las diferencias en estas tasas de
crecimiento se podría afirmar que para que el PIB per cápita regrese a la
tendencia definida como L2 en la gráfica 1 tendrían que pasar más de 19 años,
si es que tal reversión fuera posible, en tanto que para volver a la denotada
por L3 serían necesarios 13 años aproximadamente.
Conclusiones
Los resultados de este
documento no son contundentes debido a que las pruebas y metodologías
utilizadas arrojan conclusiones diferentes, situación que se complica con el
hecho de que tales pruebas y metodologías no son directamente comparables entre
sí. Sin embargo, es posible que sus implicaciones sean compatibles.
El análisis de descomposición
para el periodo completo (1921-l995), sugiere que una elevada proporción de las
variaciones corrientes del PIB per cápita real tienen un carácter permanente
(62%), lo cual introduce persistencia a la serie en la medida que su evolución
actual está afectada por sus valores pasados. Las pruebas de raíces unitarias,
realizadas para distintos subperiodos, muestran resultados divergentes. La
prueba DFA permite rechazar la hipótesis de raíz unitaria solamente en el
intervalo 1932-1981, indicando que en los demás periodos la tendencia es
estocástica y los choques son permanentes. Por su parte, la prueba PP permite
rechazar la misma hipótesis en los periodos considerados, excepto en el que va
de 1932 a 1995. Estas dos pruebas coinciden en que, una vez eliminado el
intervalo inicial acaecido en torno a la declinación resultante de la crisis
mundial del capitalismo, es decir, a partir de 1932, los efectos de la
desaceleración de la economía mexicana iniciada en la década anterior tienen un
carácter permanente que impide un retorno a su tendencia de largo plazo.
Con todo, estas pruebas han
sido colocadas en tela de juicio por su ineficacia para distinguir entre un
coeficiente autorregresivo alto pero menor a 1, y una raíz unitaria (Sims, 1988),
o por no considerar que toda serie tiene un componente permanente y uno
transitorio (Cochrane, 1988). La prueba propuesta por Sims permite concluir que
la serie no sigue un camino aleatorio en ninguno de los periodos considerados.
Con respecto al último de éstos debe resaltarse que la tendencia hacia la cual
se convergería es más aplanada, indicando una tasa de crecimiento media anual
menor. Las pruebas sugeridas por Cochrane permiten concluir que en los
intervalos 1921-1981 y 1921-1995, la serie tiene una tendencia estocástica, y
que en los periodos 1932-1981 y 1932-1995, la tendencia es determinista; por
ende, los choques se desvanecen a medida que transcurre el tiempo. Entre 1932 y
1981 se requerían 19 años para retornar a la tendencia señalada, mientras que
entre 1932 y 1995 eran necesarios 13 años para retornar a una tendencia que
implica una tasa de crecimiento media anual menor en 0.2%; para retornar a la
anterior tendencia se requerirían más de 19 años, si es que esto fuera posible.
En todo caso, al parecer
habría una lenta reversión a la tendencia que podría explicarse por la gran
importancia del componente camino aleatorio, o por la existencia de una raíz
casi unitaria (por lo que en algunos casos se rechaza la hipótesis de
existencia de una raíz unitaria) que hace que las fuerzas de reversión sean tan
débiles que no puedan detectarse en tamaños de muestra finitos (que permiten
aceptar la hipótesis de existencia de raíces unitarias), tal como han sugerido
Nelson y Plosser (1982) en el caso de muestras de 61 y 101 datos.
En resumen, a partir de las
pruebas y las metodologías empleadas se infiere que los choques que experimenta
la economía mexicana tienen tal persistencia que se requiere de la espera de
más de una década, al menos, para recuperar una tasa media de crecimiento
sostenido similar a la media histórica. Sin embargo, las exigencias de la
sociedad no pueden posponerse por un periodo tan prolongado. Evidentemente algo
puede hacerse para apresurar la recuperación de la economía. Una política económica
activa que impulse la actividad productiva de manera efectiva y eficiente, o un
arreglo en materia de deuda externa que reduzca el flujo de recursos al
exterior, son dos ejemplos que podrían constituirse en fuentes de choques
positivos con efectos que pueden permanecer en el tiempo. En ese sentido,
coincidimos con la conclusión de Ruprah (1991) respecto a que la austeridad
fiscal como respuesta al problema de la deuda puede tener efectos nocivos en el
comportamiento futuro de la economía; así como con Blanchard y Summers (1988),
quienes afirman que las políticas antiinflacionarias pueden generar una
situación de histéresis que dificulta cada vez más la recuperación del
crecimiento sostenido.
Bibliografía
Balke, S.
Natham (1991), "Modelling trends in macroeconomic time series", Economic
Review, Federal Reserve Bank of Dallas, mayo, pp. 19-33.
Banerjee,
Anindya et al. (1992), "Recursive and sequential tests of the unit-root
and trend-break hypotheses: Theory and international evidence", Journal
of Business and Economic Statistics, vol. 10, núm. 3, julio, pp. 271-287.
Beveridge,
Stephen y Charles R. Nelson (1981), "A new approach to decomposition of
economic time series into permanent and transitory components with particular
attention to measurement of business cycle'", Journal of Monetary
Economics, vol.7, pp. 151-174.
Blanchard,
Olivier Jean y Nobuhiro Kiyotaki (1987), "Monopolistic competition and the
effects of agregate demand", American Economic Review, vol. 77,
núm. 4, septiembre, pp. 647-666.
Blanchard,
Olivier Jean y Lawrence H. Summers (1988), "Beyond the natural rate
hipothesis", The American Economic Review, vol. 78, núm. 2, mayo,
pp. 182-187.
Box, G. E.
P. y G. C. Tiao (1975), "Intervention analysis with applications to
economic and environmental problems", Journal of American Statistical
Association, vol. 70, núm. 349, pp. 70-79.
Campbell,
John Y. y N. Gregory Mankiw (1987a), "Permanent and transitory components
in macroeconomic fluctuations", The American Economic Review. Papers
and Proceedings, vol. 77, núm. 2, mayo, pp. 111-117.
−−−
(1987b), "Are output fluctuations transitory?", The Quarterly
Journal of Economics, vol. CII, núm. 4, noviembre, pp. 857-879.
Cochrane,
John H. (1988), "How big is the random walk in GNP?", Journal of
Political Economy, vol. 96, núm. 51, pp. 893-920.
Cuddington,
John T. y L. Alan Winters (1987), "The Beveridge-Nelson decomposition of
economic time series. A quick computational method", Journal of
Monetary Economics, vol. 19, núm. 1, enero, pp. 125-127.
Cuddington, John T. y Carlos
M. Urzúa (1988), "Ciclos y tendencias en los términos netos de
intercambio: un nuevo enfoque", Estudios Económicos, vol. 3, núm.
2, pp. 169-190.
−−−
(1989), "Trends and cycles in Colombia's real GNP and fiscal deficit",
Journal of Development Economics, vol. 30, pp. 325-343.
Cuddington,
John T. y Hong Wei (1992), "An empirical analysis of real commodity
trends: aggregation, model selection and implications", Estudios
Económicos, vol. 7, núm. 2, pp. 159-180.
Cuthbertson,
Keith et al. (1992), Applied Econometric Techniques, Ann Arbor, Michgan,
The University of Michigan Press.
Dickey, D.
A. y W. A. Fuller (1981), "Likelihood ratio statistics for autoregresive
time series with a unit root", Econométrica, vol. 49, núm. 4,
julio, pp. 1057-1072.
Dornbusch, R. y M. H.
Simonsen (1987), "Estabilización de la inflación con el apoyo de una
política de ingresos", El Trimestre Económico, vol. LIV (2) núm. 214, abril-junio,
pp.225-282.
Durlauf,
Steven N. (1991), "Multiple equilibria and persistence in agregate
fluctuations", The American Economic Review. Papers and Proceedings,
vol. 81, núm. 2, mayo, pp. 70-75.
−−−
(1993), "Time series properties of aggregate output fluctuations", Journal
of Econometrics, vol. 56, marzo, pp. 39-56.
Escribano, Álvaro Sáez
(1990), "Introducción al tema de cointegración y tendencias", Cuadernos
Económicos del ICE, Secretaría de Estado de Comercio y Ministerio de
Economía y Hacienda, Barcelona, núm. 4, pp. 7-42.
Frisch,
Helmut (1986), Theories of Inflation, Cambridge, Cambridge University
Press.
Fuller, W.
A. (1976), Introduction to Statistical Time Series, Nueva York, John
Wiley and Sons.
Granger,
Clive W. J. (1993), "What are we learning about the long-run?", The
Economic Journal, vol. 103, marzo, pp. 307-317.
Guerrero
García, Víctor Manuel (1991), Análisis estadístico de series de tiempo
económicas, México, UAM-Iztapalapa.
Haan, Jakob de y Dick Zelhorst (1993), "Does output have a unit
root? New international evidence", Applied Economics, vol. 25,
julio, pp. 953-960.
Harvey,
Andrew (198 l), Time Series Models, Londres, Phillip Allan.
−−−
(1991)) The Econometric Analysis of Time Series, Cambridge,
Massachusetts, MIT Press, segunda edición.
Hernández Veleros, Zeus
Salvador (1995), Una breve reseña sobre raíces unitarias y algunas pruebas
aplicadas al PIB per cápita de México, México, CIDE, tesis de maestría en
economía.
Herrera, Santiago (1990),
"Notas sobre la existencia de una raíz unitaria en la serie del tipo de
cambio real del peso colombiano", Estudios Económicos, vol. 5, núm.
1, pp. 157-171.
Jarque, Carlos M. y Luis
Téllez K. (1993), El combate a la inflación. El éxito de la fórmula mexicana,
México, Grijalbo.
Judge, G. George et al. (1985), Introduction to the Theory
and Econometric Practice, Nueva York, John Wiley and Sons, segunda edición.
Mankiw, N. Gregory (1992),
"Un curso rápido sobre macroeconomía", Investigación Económica,
núm. 201, julio-septiembre, pp. 243-269.
Mejía Reyes, Pablo y José C.
González Núñez (1996), "La paridad del poder de compra en el largo plazo:
el caso de México", Economía Mexicana, nueva época, vol. V, núm. 1, primer semestre, pp.
37-62.
Mills,
Terrence C. (1990), Time Series Techniques for Economists, Cambridge,
Cambridge University Press.
Moscan, J.
(1994), "Is there a unit root in US real GNP?", Economic Letters,
vol. 45, pp. 23-31.
Nelson,
Charles R. y Charles I. Plosser (1982), "Trends and ramdom walks in
macroeconomic time series: Some evidence and implications", Journal of
Monetary Economics, vol. 10, núm. 9, septiembre, pp. 139-62.
Pantula, Sastry G. et al.
(1994), "A comparison of
unit root test criteria", Journal of Business and Economic Statistics,
vol. 12, núm. 4, octubre, pp. 449-459.
Perron,
Pierre (1988), "Trends and random walks in macroeconomic time
series", Journal of Economic Dynamics and Control, vol. 12, pp.
297-332.
Phillips,
P. C. B. (1987), "Time series regression with a unit root", Econométrica,
vol. 55, núm. 2, marzo, pp. 277-301.
Redebusch,
Glenn D. (1993), "The uncertain unit root in real GNP", American
Economic Review, vol. 83, núm. 1, marzo, pp. 264-272.
Ros, Jaime
(1987), "Mexico from the oil boom to the debt crisis: An analysis of
policy responses to external shocks, 1978-1985", en Rosemary Thorp y
Laurence Whitehead (comps.), Latin American Debt and Adjustment Crisis,
Pittsburg, Pensilvania, University of Pittsburgh Press.
Ruprah,
Inder (1991), "¿Declinación o histéresis? El caso mexicano", El
Trimestre Económico, vol. LVIII(4),
núm. 232, octubre-diciembre, pp. 759-768.
Sims,
Christopher A. (1988), "Bayesian skepticism on unit root
econometrics", Journal of Economic Dynamics and Control, vol. 12,
pp. 463-474.
−−−y Harold
Uhlig (1991), "Understanding unit rooters: a helicopter tour", Econométrica,
vol. 59, núm. 6, noviembre, pp. 1591-1599.
West,
Kenneth D. (1988), "On the interpretation of near random-walk behavior in
GNP", American Economic Review, vol. 78, núm. 1, marzo, pp.
202-209.
Whitt,
Joseph A. Jr. (1992), "The long-run behavior of the real exchange rate: A
reconsideration", Journal of Money, Credit and Banking, vol. 24,
núm. 1, febrero, pp. 72-82.